Home
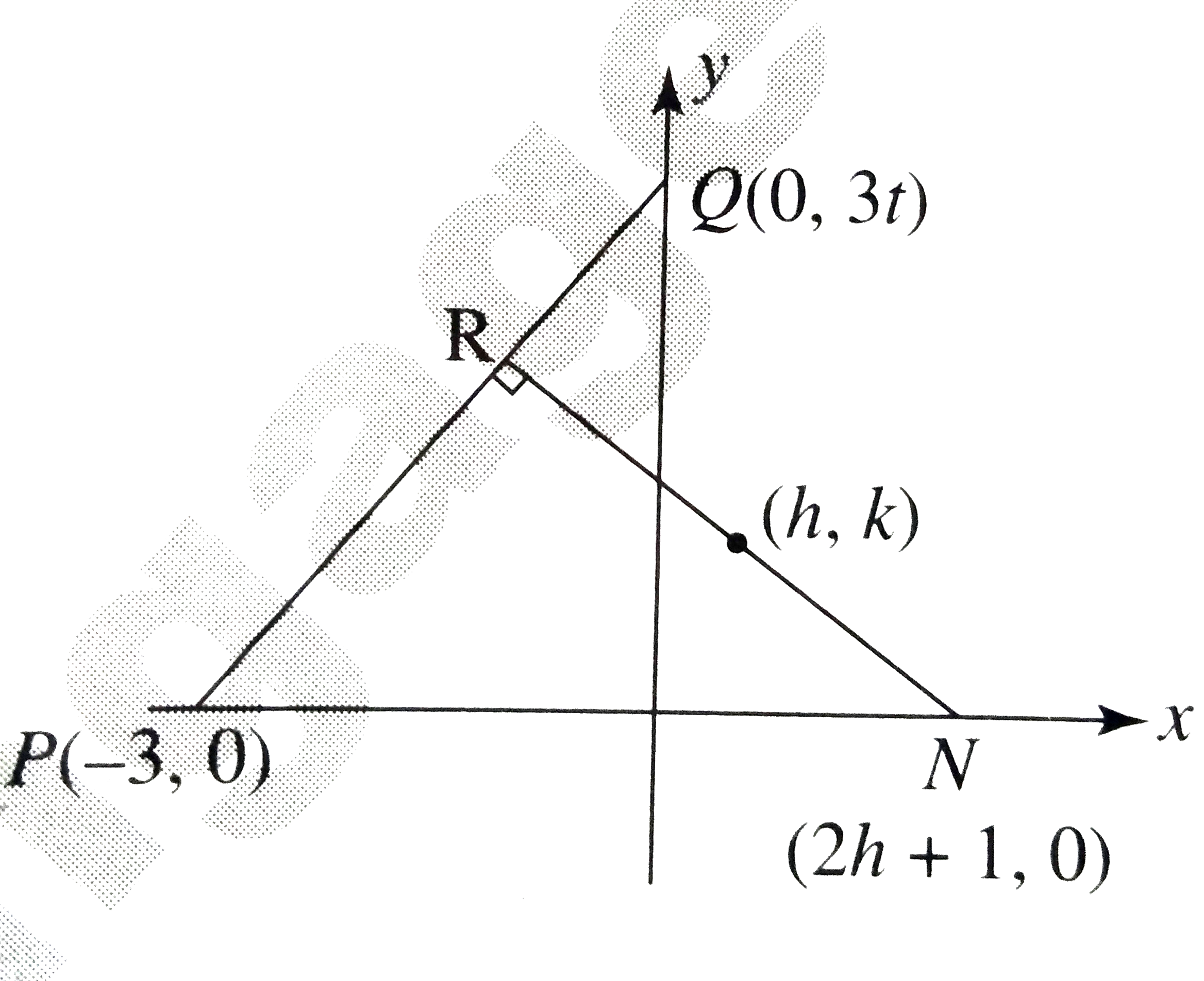
Class 12
MATHS
Let P be the point (-3,0) and Q be a mov...

Let P be the point `(-3,0)` and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the mid-point of RN is

A

`(x+3)^(2)-3y = 0`

B

`(y+3)^(2)-3x = 0`

C

`x^(2)-y = 1`

D

`y^(2)-x = 1`

Text Solution

Verified by Experts

The correct Answer is:
D

`P(-3,0), Q(0,3t), R(-1,2t)`
Let the mid point of RN be (h,k)
`:. k = t`.
`RN _|_ PQ rArr (2t)/(-2h-2) xx (3t)/(3) =-1`
`rArr 2t^(2)=2h +2`
`rArr t^(2)=h+1`
`rArr k^(2)=h +1`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSTEM

    CENGAGE PUBLICATION|Exercise Comprehension Type|4 Videos

  • COORDINATE SYSTEM

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 Videos

  • CONTINUITY AND DIFFERENTIABILITY

    CENGAGE PUBLICATION|Exercise All Questions|238 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise JEE Main|6 Videos

Similar Questions

Explore conceptually related problems

Let A be the fixed point (0, 4) and B be a moving point on x-axis. Let M be the midpoint of AB and let the perpendicular bisector of AB meets the y-axis at R. The locus of the midpoint P of MR is

Let P be the point (1,0) and Q be a point on the locus y^(2)=8x . The locus of the midpoint of PQ is

let P be the point (1, 0) and Q be a point on the locus y^2= 8x . The locus of the midpoint of PQ is

P,Q and R three points on the parabola y^(2)=4ax . If Pq passes through the focus and PR is perpendicular to the axis of the parabola, show that the locus of the mid point of QR is y^(2)=2a(x+a) .

A line cuts the x-axis at A(5,0) and the y-axis at B(0,-3). A variable line PQ is drawn perpendicular to AB cutting the x-axis at P and the y-axis at Q. If AQ and BP meet at R, then the locus of R is

Let A be any variable point on the X-axis and B the point (2,3). The perpendicular at A to the line AB meets the Y-axis at C. Then the locus of the mid-point of the segment AC as A moves is given by the equation

Let P be the point (1,0) and Q a point on the parabola y^(2) =8x, then the locus of mid-point of bar(PQ is-

Find the equation of the plane passing through the points (2,1,0),(5,0,1) and (4,1,1) If P is the point (2,1,6) then find point Q such that PQ is perpendicular to the above plane and the mid point of PQ lies on it.

A striaght line intersect x-axis at A(7,0) and y-axis at B(0,-5). The straight line PQ is perpendicular to AB and intersect the x and y-axes at P adn Q respectively. Find the eqution to the locus of the point of intersection of the line AQ and BP.

A line cuts the x-axis at A (7, 0) and the y-axis at B(0, - 5) A variable line PQ is drawn perpendicular to AB cutting the x-axis in P and the y-axis in Q. If AQ and BP intersect at R, find the locus of R.