Home
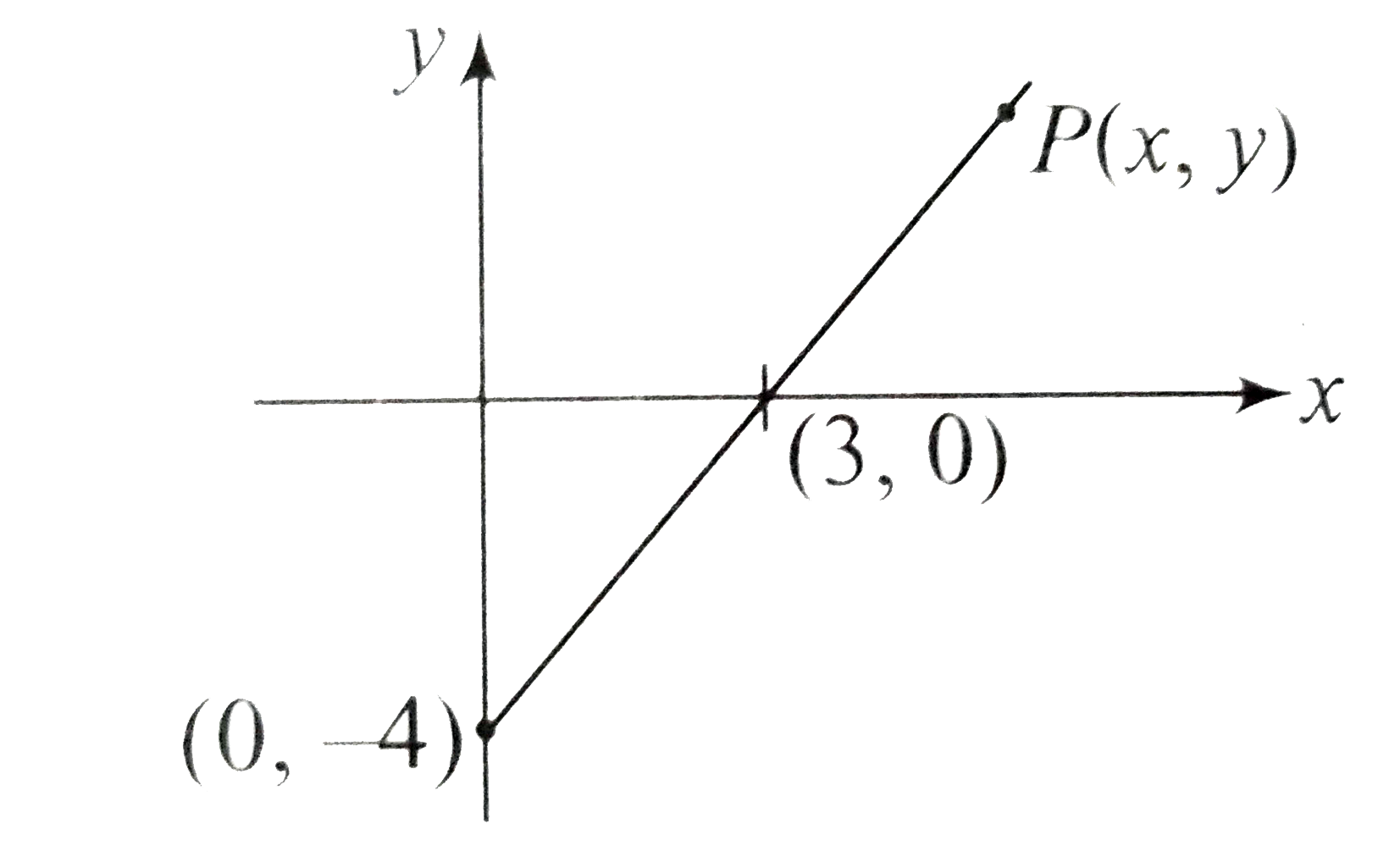
Class 12
MATHS
The locus of P(x,y) such that sqrt(x^2+...

The locus of `P(x,y)` such that `sqrt(x^2+y^2+8y+16)-sqrt(x^2+y^2-6x+9)=5,` is

A

A. hyperbola

B

B. circle

C

C. finite line segment

D

D. infinite ray

Text Solution

Verified by Experts

The correct Answer is:
D
We have `sqrt(x^(2)+(y+4)^(2)) -sqrt((x-3)^(2)-y^(2))=5`. The distance between the two points (3,0) and `(0,-4)` is 5.

Locus of P is the part of line `(x)/(3) -(y)/(4) =1`.
Promotional Banner

Similar Questions

Explore conceptually related problems

The locus of the point P(x,y) satisfying the relation sqrt((x-3) ^(2) +(y-1)^(2))+ sqrt((x+3) ^(2) +(y-1)^(2))=6 is-

The equation sqrt({(x-2)^2+y^2})+sqrt({(x+2)^2+y^2})=4 represents

The solution of (x d x+y dy)/(x dy-y dx)=sqrt((1-x^2-y^2)/(x^2+y^2)) is

A common tangent to 9x^2-16y^2 = 144 and x^2 + y^2 = 9 , is

If x>y prove that sqrt(y+sqrt(2xy-x^2))+sqrt(y-sqrt(2xy-x^2)) = sqrt(2x) .

If y=(x+sqrt(x^2+a^2))^n ,t h e n(dy)/(dx) is (a) (n y)/(sqrt(x^2+a^2)) (b) -(n y)/(sqrt(x^2+a^2)) (c) (n x)/(sqrt(x^2+a^2)) (d) -(n x)/(sqrt(x^2+a^2))

A variable chord of the circle x^2+y^2=4 is drawn from the point P(3,5) meeting the circle at the point A and Bdot A point Q is taken on the chord such that 2P Q=P A+P B . The locus of Q is (a) x^2+y^2+3x+4y=0 (b) x^2+y^2=36 (c) x^2+y^2=16 (d) x^2+y^2-3x-5y=0

The equation |sqrt(x^(2)+(y-1)^(2))-sqrt(x^(2) +(y+1)^(2))| = k will represent a hyperbola for-

Find the locus of a point which moves so that the ratio of the lengths of the tangents to the circles x^2+y^2+4x+3=0 and x^2+y^2-6x+5=0 is 2: 3.

The locus of a point that is equidistant from the lines x+y - 2sqrt2 = 0 and x + y - sqrt2 = 0 is (a) x+y-5sqrt2=0 (b) x+y-3sqrt2=0 (c) 2x+2y-3 sqrt2=0 (d) 2x+2y-5sqrt5=0