Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
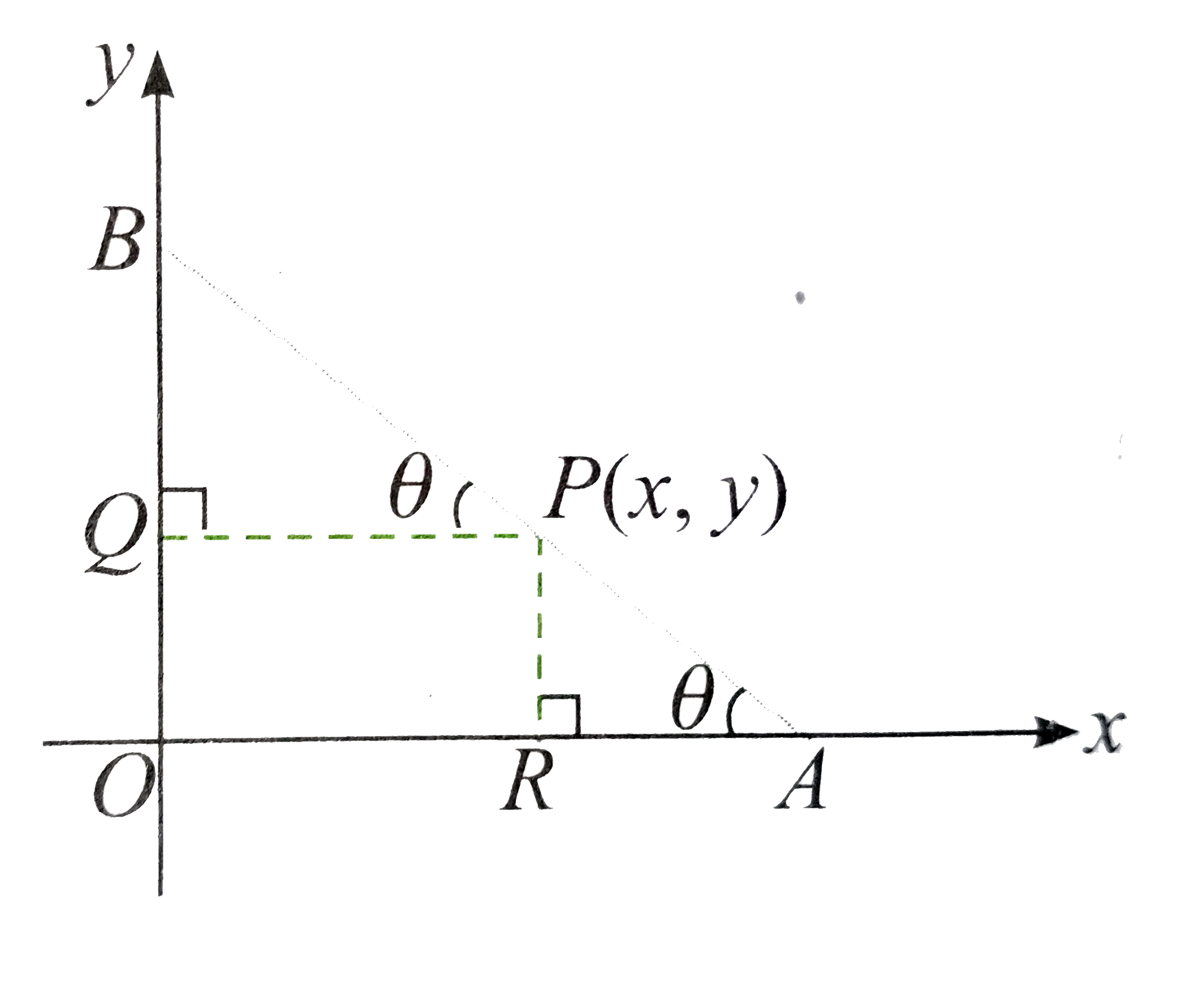
- A rod of length l cm moves with its ends A (on x=-axis) and B (on y-ax...
Text Solution
|
- A rod of length l cm moves with its ends A (on x=-axis) and B (on y-ax...
Text Solution
|
- A rod of length 1.2 m moves with its ends always touching the coordin...
Text Solution
|
- Express each of the following decimals in the p/q form 7.35
Text Solution
|
- A rod AB of length 15 cm rests in between two coordinate axes is such ...
Text Solution
|
- A rod of length 12 cm moves with its ends always touching the coordina...
Text Solution
|
- A rod AB of length 15 cm rests in between two coordinate axes is such ...
Text Solution
|
- A rod of length 12 cm moves with its ends always touching the coordina...
Text Solution
|
- A rod of length 12 cm moves with its ends always touching the coordina...
Text Solution
|