Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
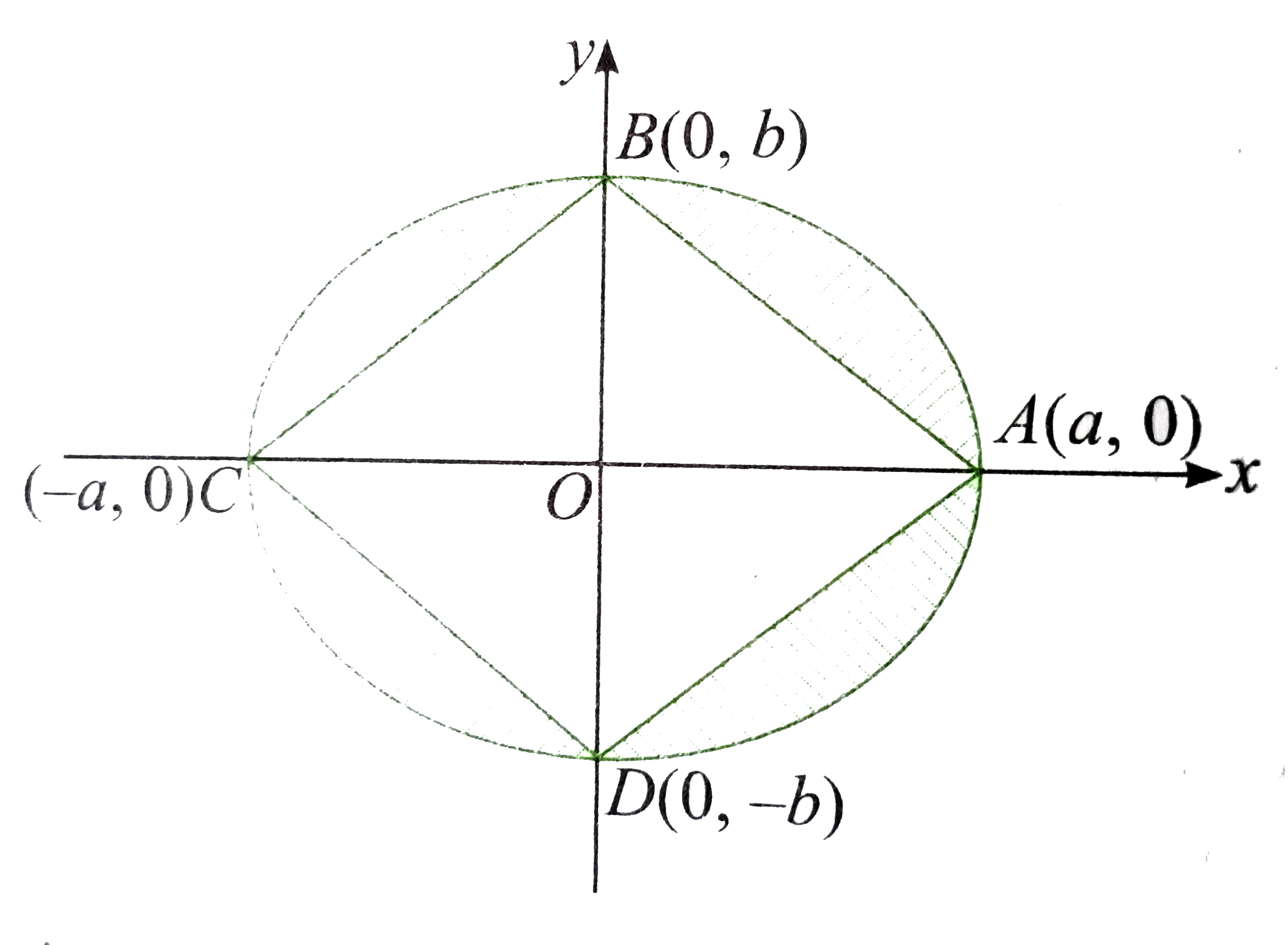
- Find the area of the smaller region bounded by the ellipse (x^2)/(a^2)...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/(a^2...
Text Solution
|
- Find the area of the smaller region bounded by the ellips (x^(2) )/(a^...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^(2))/(a^...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse x^(2)/a^(2)...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse x^(2)/a^(2)...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/(a^2...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse x^(2)/a^(2)...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^(2))/(a^...
Text Solution
|