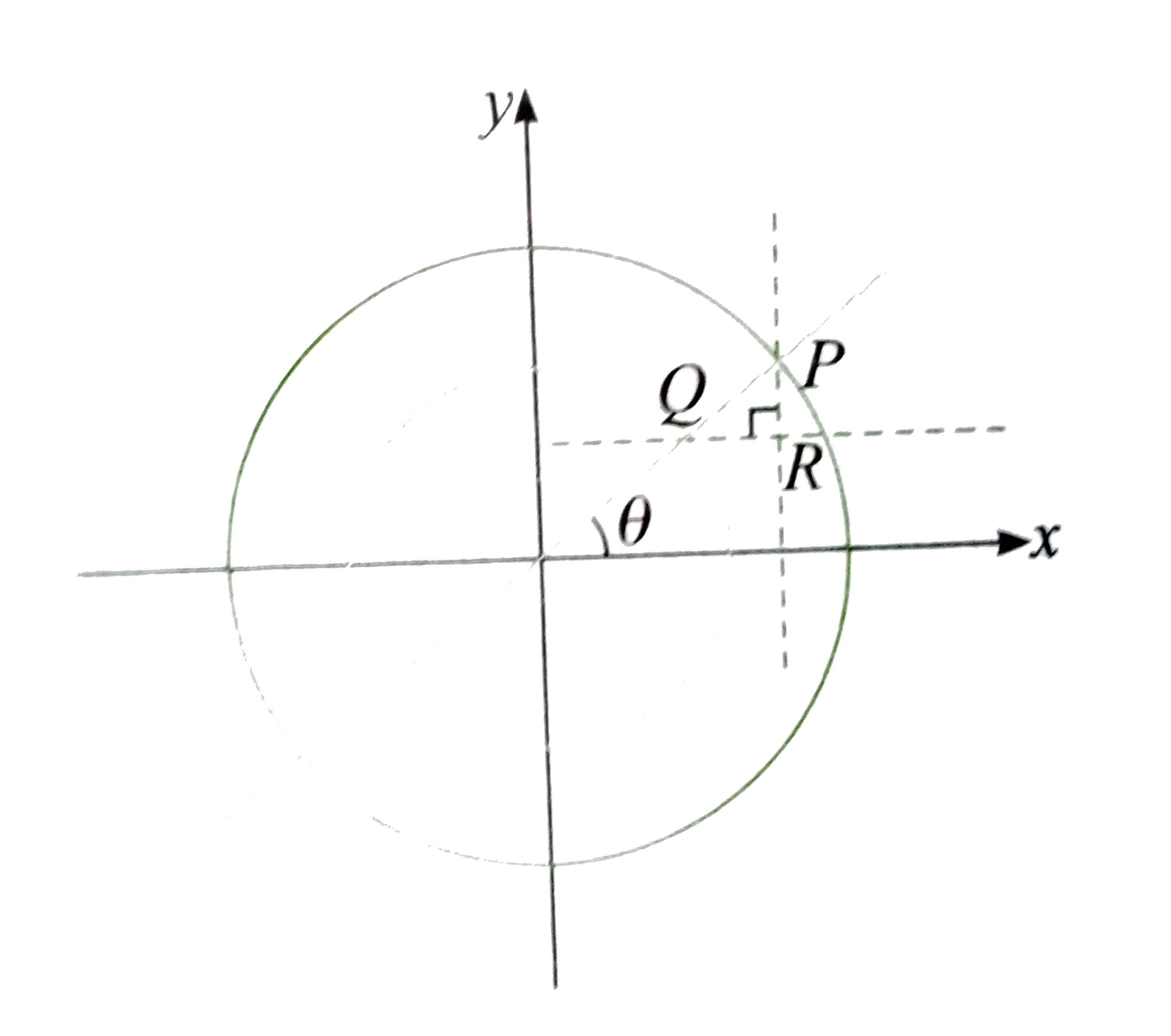
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A line passing through the origin O(0,0) intersects two concentric ...
Text Solution
|
- Two circles C1a n dC2 intersect at two distinct points Pa n dQ in a li...
Text Solution
|
- A line passing through the origin O(0,0) intersects two concentric ...
Text Solution
|
- The locus of the centre of the circle passing through the origin O an...
Text Solution
|
- A line is at a distance c from origin and meets axes in A an dB. The l...
Text Solution
|
- Two circles C1 and C2 intersect at two distinct points PandQ in a line...
Text Solution
|
- Two circles C1a n dC2 intersect at two distinct points Pa n dQ in a li...
Text Solution
|
- A line passing through the origin O(0,0) intersects two concentric ...
Text Solution
|
- A straight line passing through P(3,1) meets the coordinate axes at Aa...
Text Solution
|