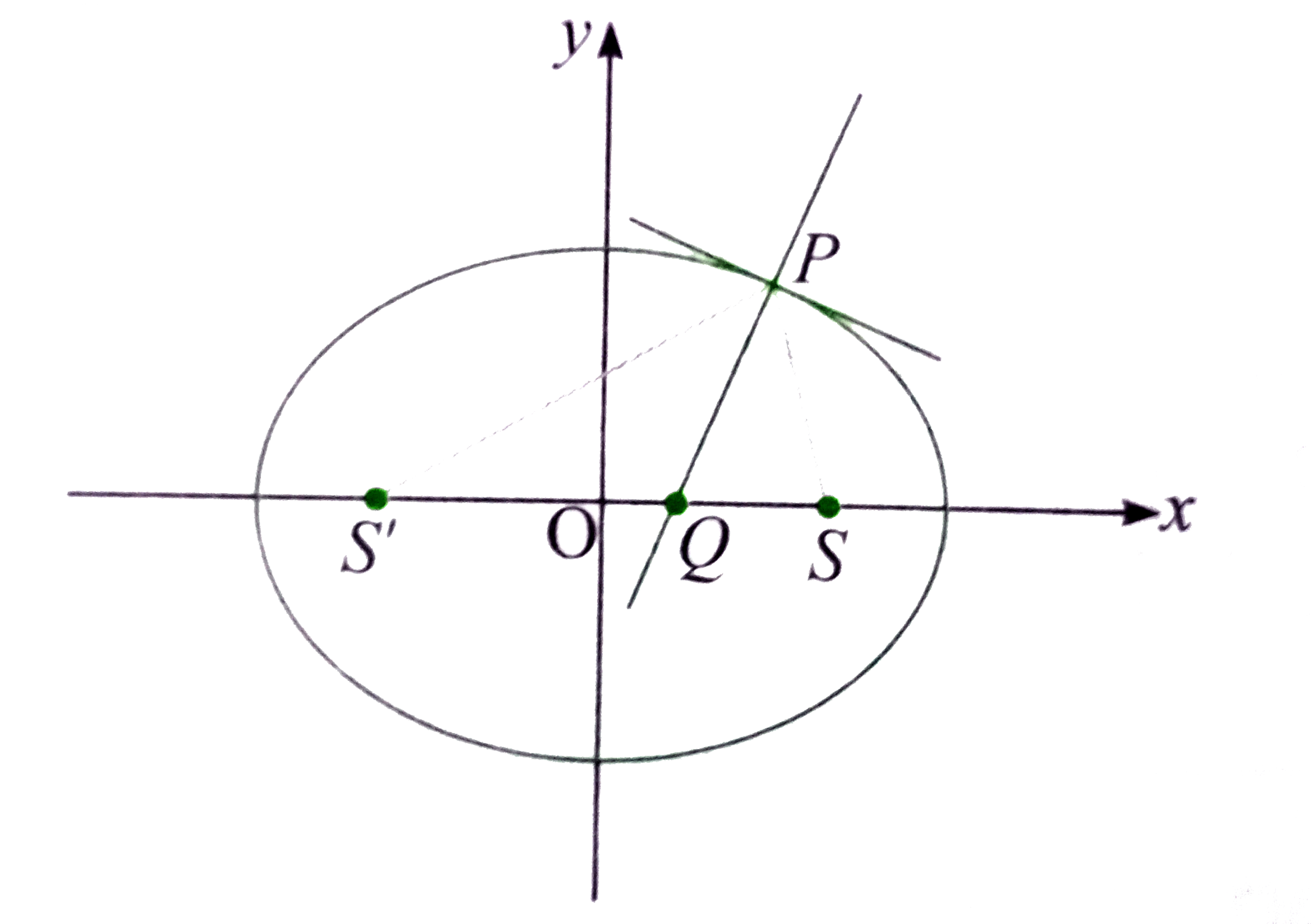
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the normal at P(2(3sqrt(3))/2) meets the major axis of ellipse (...
Text Solution
|
- If the normal at P(2,(3sqrt(3))/2) meets the major axis of ellipse...
Text Solution
|
- If P is any point on the ellipse x^(2)/36 +y^(2)/16=1 and S and S', a...
Text Solution
|
- If the normal at P(theta) on the ellipse x^(2)/a^(2)+y^(2)/b^(2)=1 wit...
Text Solution
|
- If P is any point on the ellipse (x^(2))/(36) + (y^(2))/(16) = 1 , and...
Text Solution
|
- P is a point on the ellipse (x^(2))/(36)+(y^(2))/(9)=1; S,S^(1) are ...
Text Solution
|
- P is a point on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 S and S...
Text Solution
|
- If Sa n dS ' are two foci of ellipse 16 x^2+25 y^2=400 and P S Q is ...
Text Solution
|
- If the normal at P(2,(3sqrt(3))/2) meets the major axis of ellipse...
Text Solution
|