Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
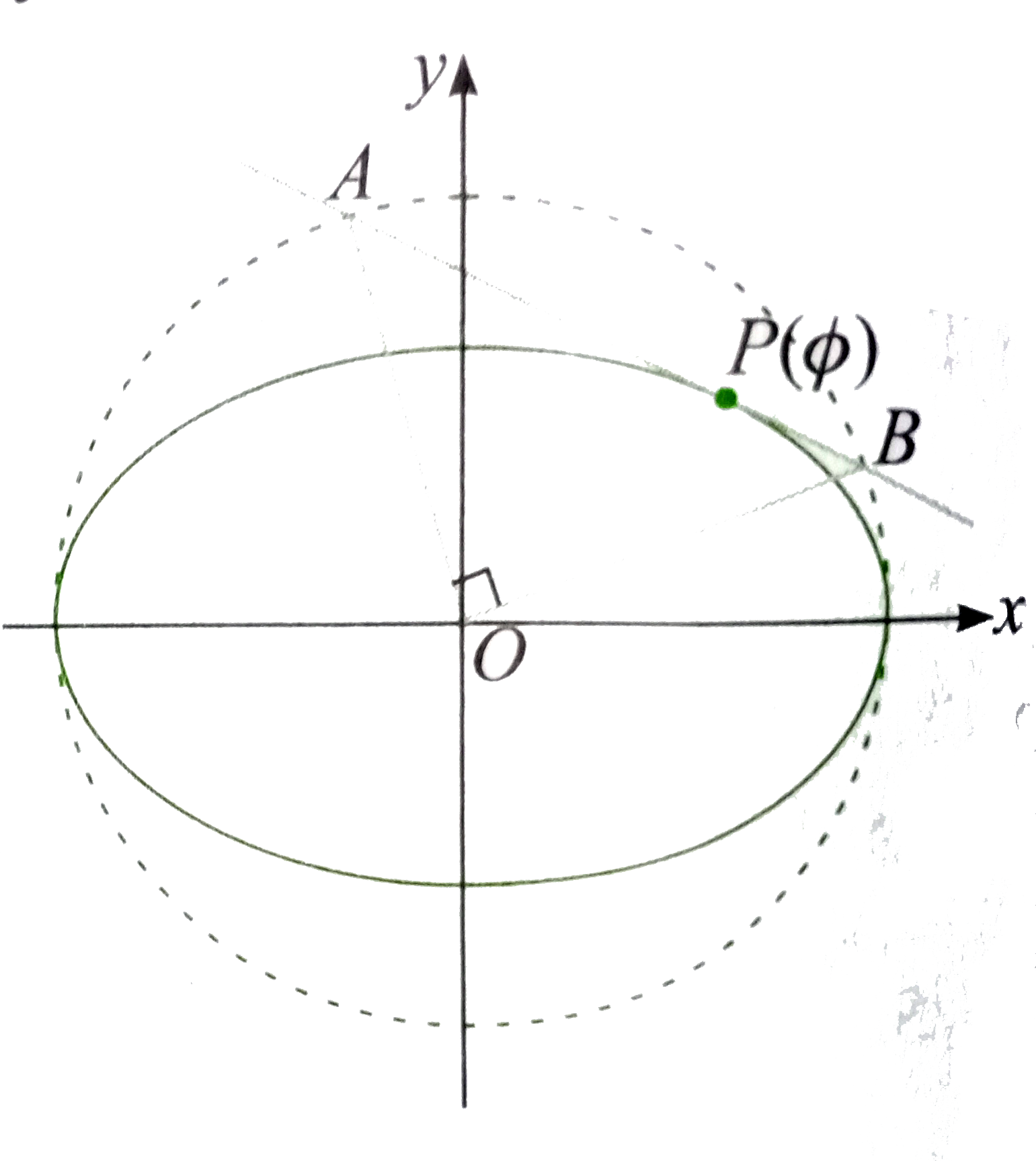
- The tangent at a point P(acosvarphi,bsinvarphi) of the ellipse (x^2)/(...
Text Solution
|
- The tangent at a point P(acosvarphi,bsinvarphi) of the ellipse (x^2)/(...
Text Solution
|
- Find the range of eccentricity of the ellipse (x^(2))/(a^(2))+(y^(2))/...
Text Solution
|
- The tangent at the point alpha on a standard ellipse meets the auxilia...
Text Solution
|
- Find the locus of middle points of chords of the ellipse (x^(2))/(a^(2...
Text Solution
|
- The tangent at the point theta on the ellipse (x^(2))/(a^(2))+(y^(2))/...
Text Solution
|
- The intercept made by the auxiliary circle of the ellipse (x ^(2))/(a ...
Text Solution
|
- " Eccentricity of ellipse "(x^(2))/(a^(2))+(y^(2))/(b^(2))=1" such tha...
Text Solution
|
- If the tangent at theta on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))...
Text Solution
|