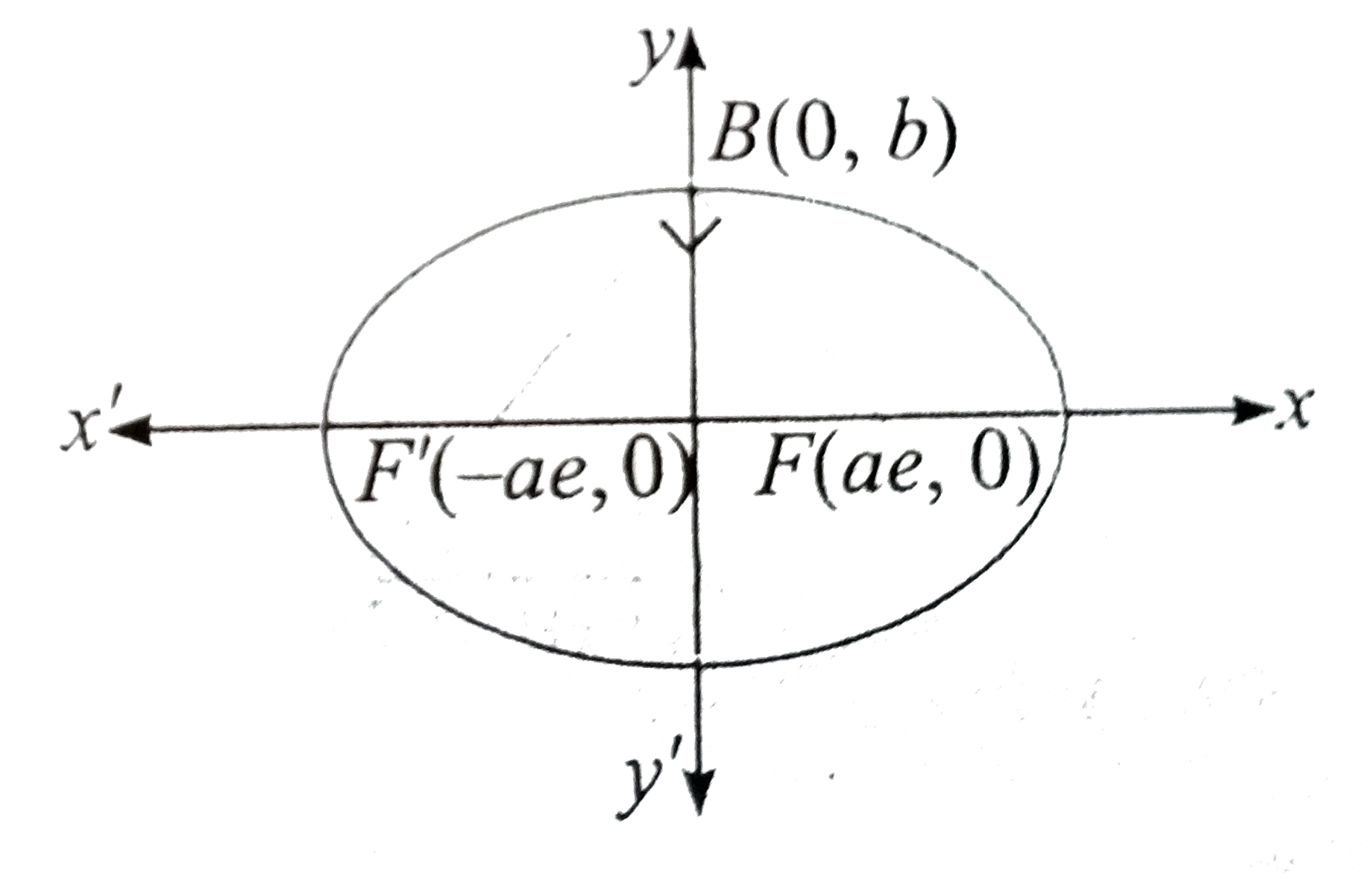Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An ellipse has O B as the semi-minor axis, Fa n dF ' as its foci...
Text Solution
|
- An ellipse has O B as the semi-minor axis, Fa n dF ' as its foci...
Text Solution
|
- OB एक दीर्घवृत्त की अर्द्ध लघु अक्ष है F तथा F' उसकी नाभियाँ है तथा an...
Text Solution
|
- Let S and s' be the foci of an ellipse and B be one end of its minor a...
Text Solution
|
- If the lines joining the foci of an ellipse to an end of its minor axi...
Text Solution
|
- An ellipse has OB, as semi minor axis, F and F' its foci and the angle...
Text Solution
|
- If OT is the semi- minor axis of an ellipse A and B are its foci and ...
Text Solution
|
- Let S and s' be the foci of an ellipse and B be one end of it...
Text Solution
|
- Let S and s' be the foci of an ellipse and B be one end of it...
Text Solution
|