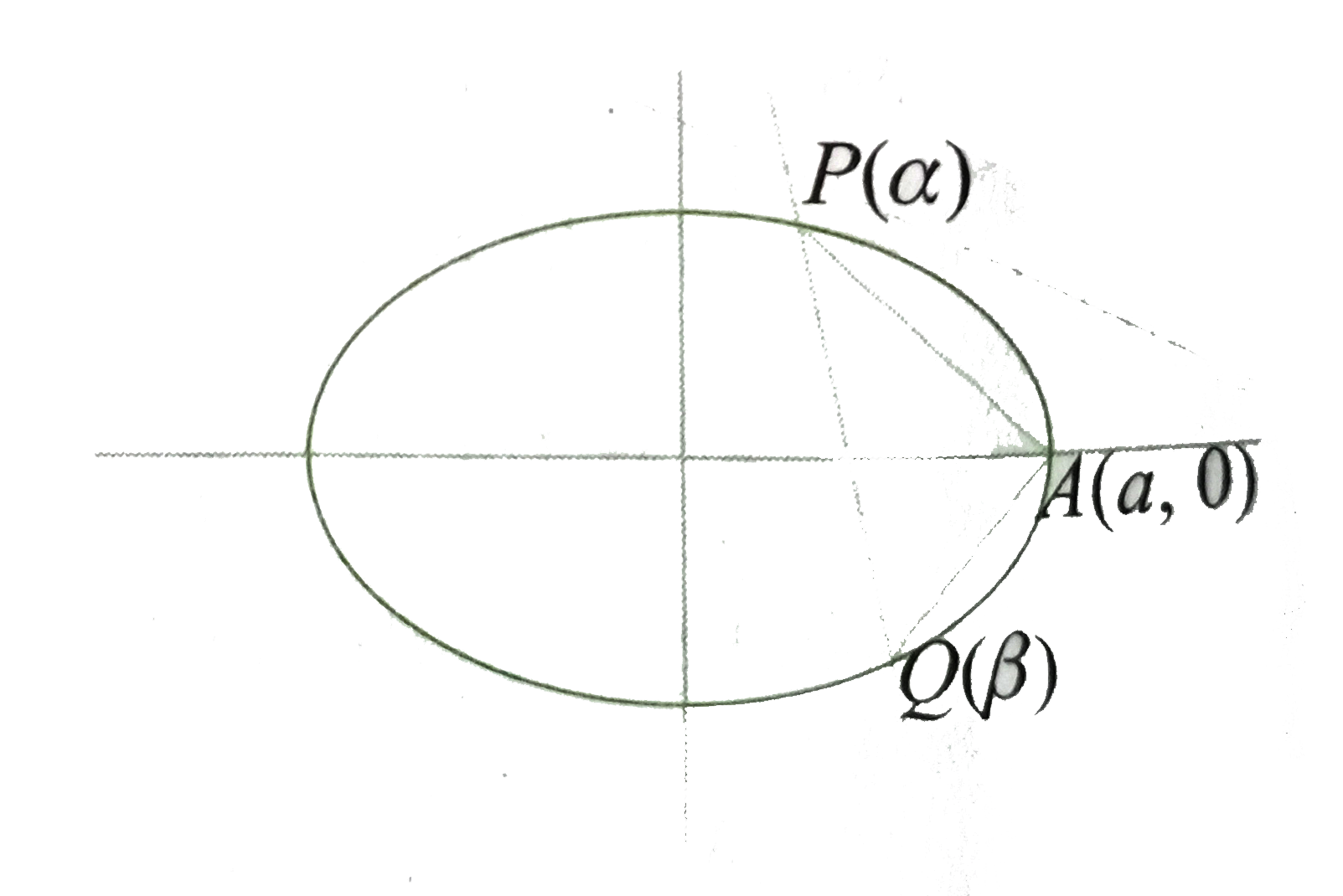Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the chord joining points P(alpha) and Q(beta) on the ellipse ((x^...
Text Solution
|
- If the chord joining points P(alpha)a n dQ(beta) on the ellipse ((x...
Text Solution
|
- If a chord joining two points whose eccentric angles are alpha and bet...
Text Solution
|
- P is any point lying on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1(...
Text Solution
|
- सिद्ध कीजिए - tan^(-1).(2ab)/(a^(2)-b^(2))+tan^(-1).(2xy)/(x^(2)-y^(2...
Text Solution
|
- Prove that the equation of the chord joining the points alpha and beta...
Text Solution
|
- If (alpha-beta)=(pi)/(2) ,then the chord joining the points whose ec...
Text Solution
|
- IF alpha , beta are eccentric angles of end points of a focal cho...
Text Solution
|
- If tanalphatanbeta=-(a^(2))/(b^(2)), then the chord joining the points...
Text Solution
|