Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
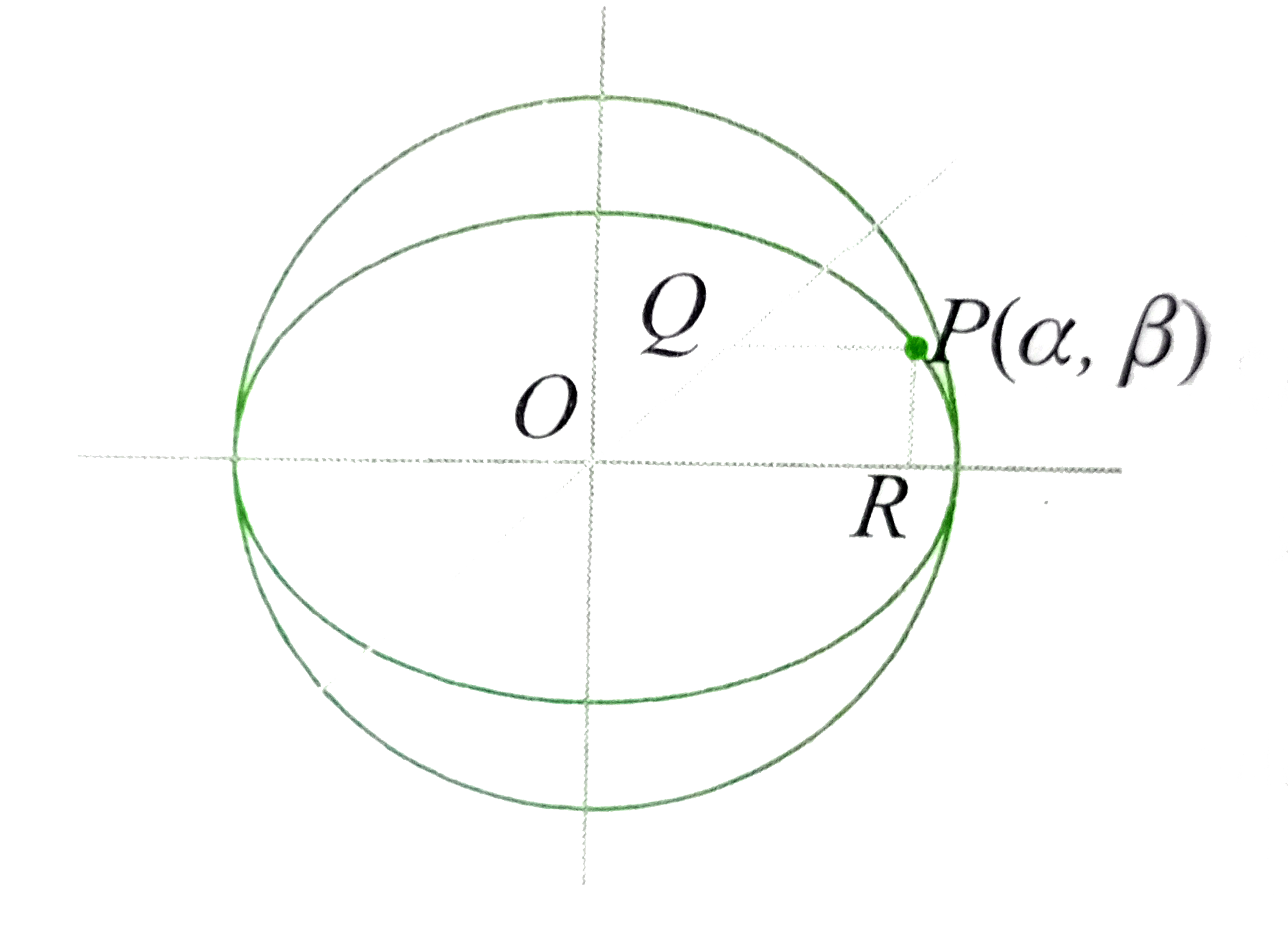
- Find the point (alpha,)beta on the ellipse 4x^2+3y^2=12 , in the first...
Text Solution
|
- Find the point (alpha,beta) on the ellipse 4x^2+3y^2=12 , in the first...
Text Solution
|
- the lines x+y+1=0;4x+3y+4=0 and x+alpha y+beta=0, where alpha^(2)+beta...
Text Solution
|
- Let alpha be the distance between the lines x-y+2=0 and x-y =2 and bet...
Text Solution
|
- यदि sin alpha + sin beta = x तथा cos alpha + cos beta = y, तो सिद्ध ...
Text Solution
|
- If x cos alpha + y sin alpha = x cos beta + y sin beta "then" "tan" ...
Text Solution
|
- Ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 On (alpha, beta) The tangent...
Text Solution
|
- Find the point (alpha,beta) on the ellipse 4x^2+3y^2=12 , in the first...
Text Solution
|
- In the first quadrant, the x-axis, the line y = x and the circle x^(2)...
Text Solution
|