Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
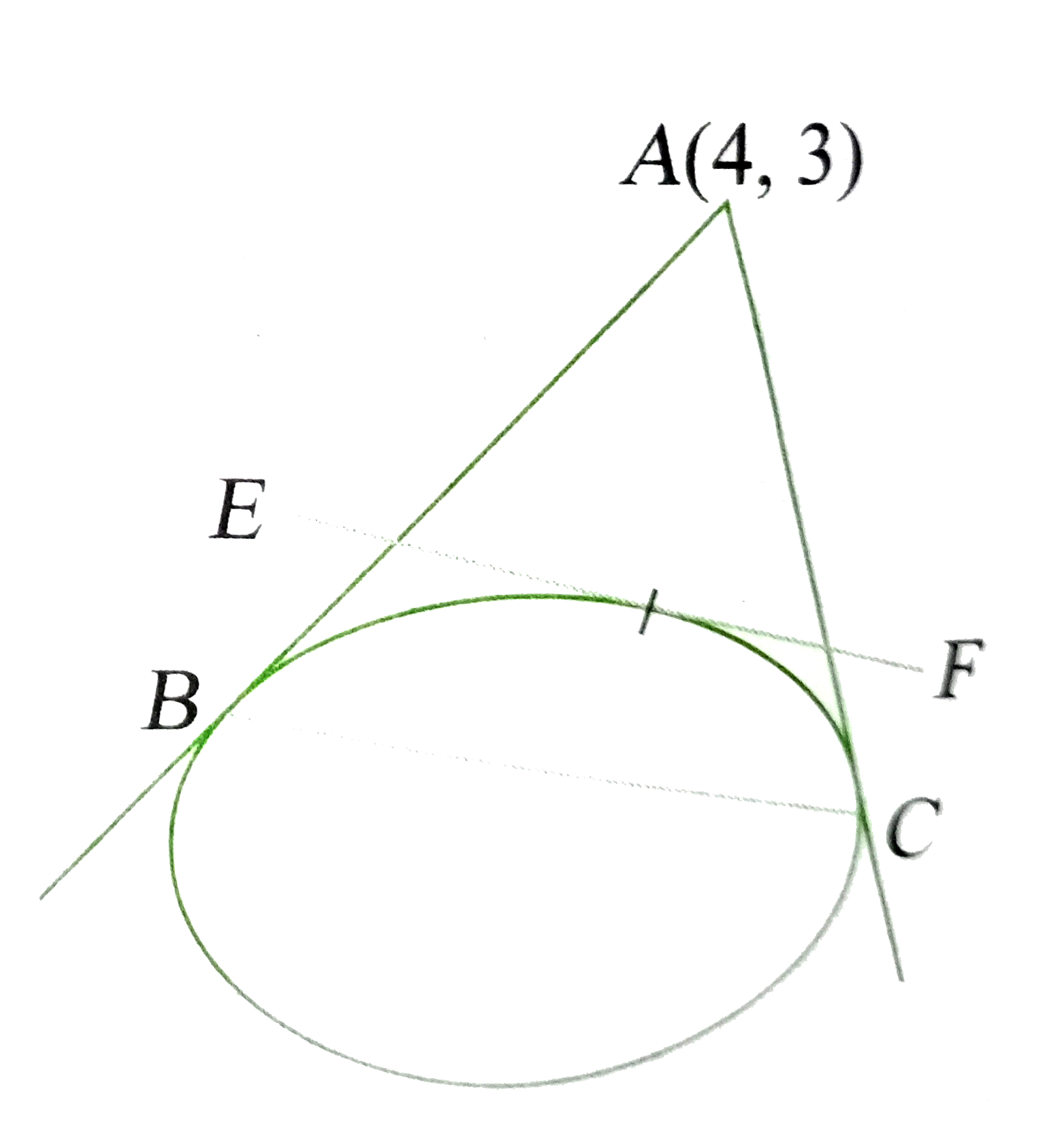
- From the point A(4,3), tangent are drawn to the ellipse (x^2)/(16)+...
Text Solution
|
- From the point A(4,3), tangent are drawn to the ellipse (x^2)/(16)...
Text Solution
|
- Tangents are drawn from the point P(3,4) to the ellipse (x^(2))/(9)+(y...
Text Solution
|
- Tangents are drawn from the point P(3,4) to the ellipse x^2/9+y^2/4=1...
Text Solution
|
- Tangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/...
Text Solution
|
- Tangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/...
Text Solution
|
- Tangents are drawn from the point P(3, 4) to the ellipse x^2/9 +y^2/4 ...
Text Solution
|
- Given the ellipse (x ^(2))/(4) +y ^(2) =1, the point on the line x =2,...
Text Solution
|
- Ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 The point of the foot of the...
Text Solution
|