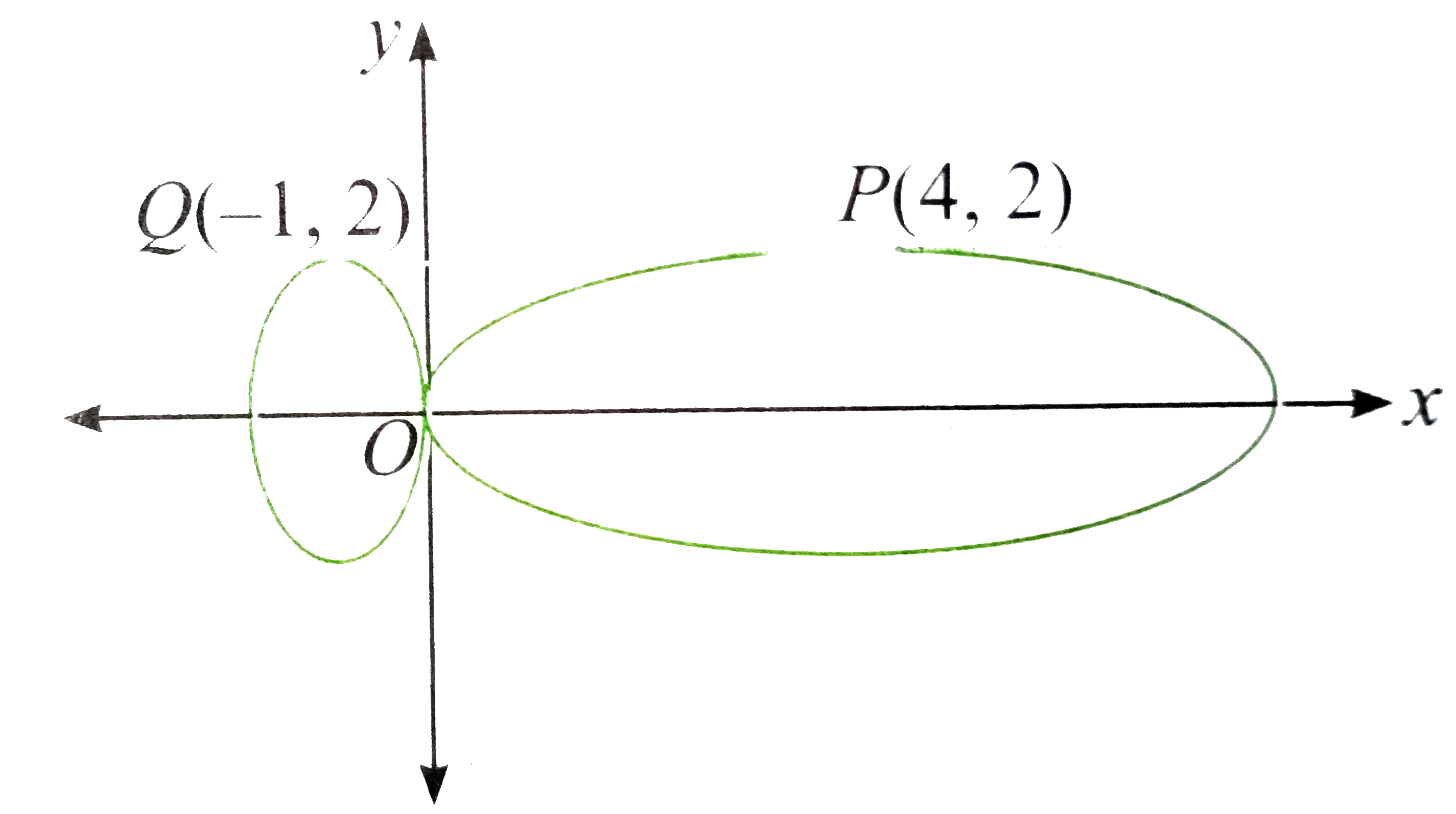
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The angle subtended by common tangents of two ellipses 4(x-4)^2+25 y^2...
Text Solution
|
- The angle between the two tangents from the origin to the circle (x-7)...
Text Solution
|
- tan^(-1)(x/y)-tan^(-1)((x-y)/(x+y)) is (A) pi/2 (B) pi/3 (C) pi/4 ...
Text Solution
|
- If (sinx)(cosy)=1/2, then (d^2y)/(dx^2) at (pi/4,pi/4) is (a) -4 (b) -...
Text Solution
|
- The line tangent to the curves y^3-x^2y+5y-2x=0 and x^2-x^3y^2+5x+2y=0...
Text Solution
|
- The angles at which the circles (x-1)^2+y^2=10a n dx^2+(y-2)^2=5 inte...
Text Solution
|
- The angle subtended by common tangents of two ellipses 4(x-4)^2+25 y^2...
Text Solution
|
- Tangents drawn from a point on the circle x^(2)+y^(2)=9 to the hyperbo...
Text Solution
|
- The angle of intersection of the parabola y^2=4\ a x and x^2=4a y a...
Text Solution
|