A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
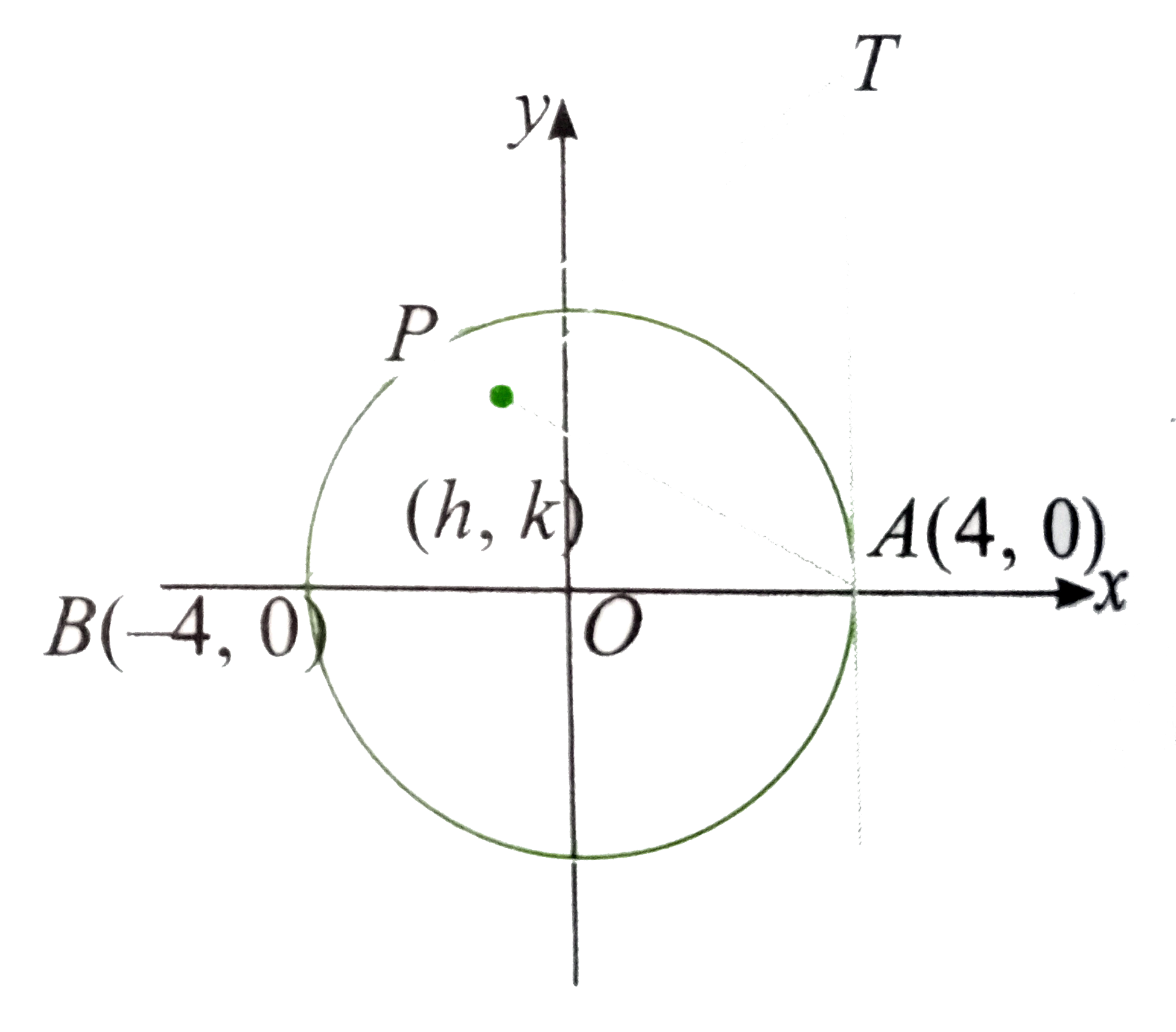
- The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tang...
Text Solution
|
- The tangent at any point P of a circle x^(2)+y^(2)=a^(2) meets the tan...
Text Solution
|
- If 'P' be a moving point on the ellipse (x^(2))/(25)+(y^(2))/(16)=1 in...
Text Solution
|
- The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tang...
Text Solution
|
- The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tang...
Text Solution
|
- The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tang...
Text Solution
|
- A variable circle passes through the fixed point A(p,q) and touches t...
Text Solution
|
- A line through the origin meets the circle x^(2) +y^(2) =a^(2) at P ...
Text Solution
|
- A variable circle passes through the fixed point A (p, q) and touches ...
Text Solution
|