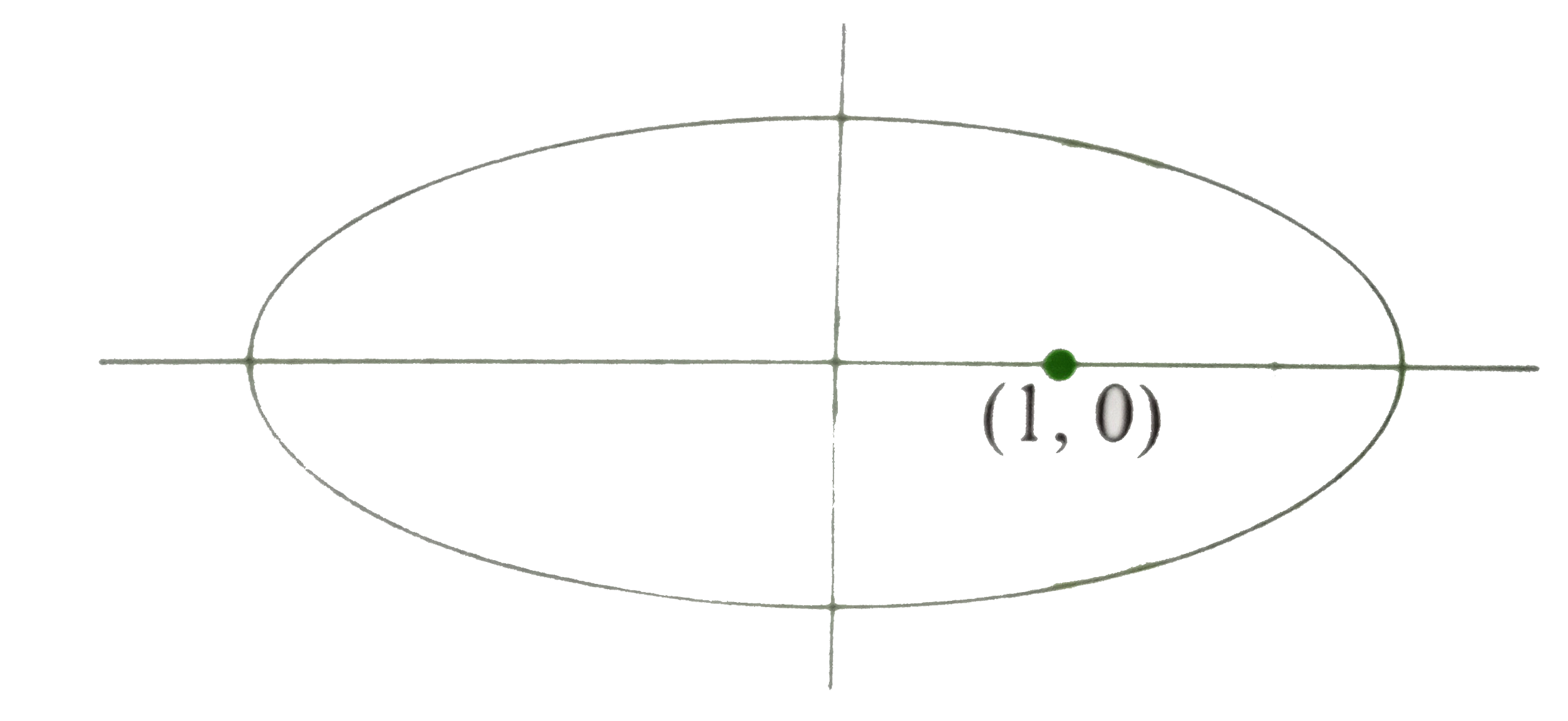
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that it has the...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse x^(2)/169+y^(2)/25=1 has the same eccentricity as the elli...
Text Solution
|
- If the area of the auxiliary circle of the ellipse (x ^(2))/(a ^(2)) +...
Text Solution
|
- The ellipse (x^(2))/(169) + (y^(2))/(25) = 1 has the same eccentri...
Text Solution
|
- Determine the equation of the ellipse x^(2)/a^(2)+y^(2)/b^(2) = 1 suc...
Text Solution
|
- If the area of the auxillary circle of the ellipse (x^(2))/(a^(2)) + (...
Text Solution
|