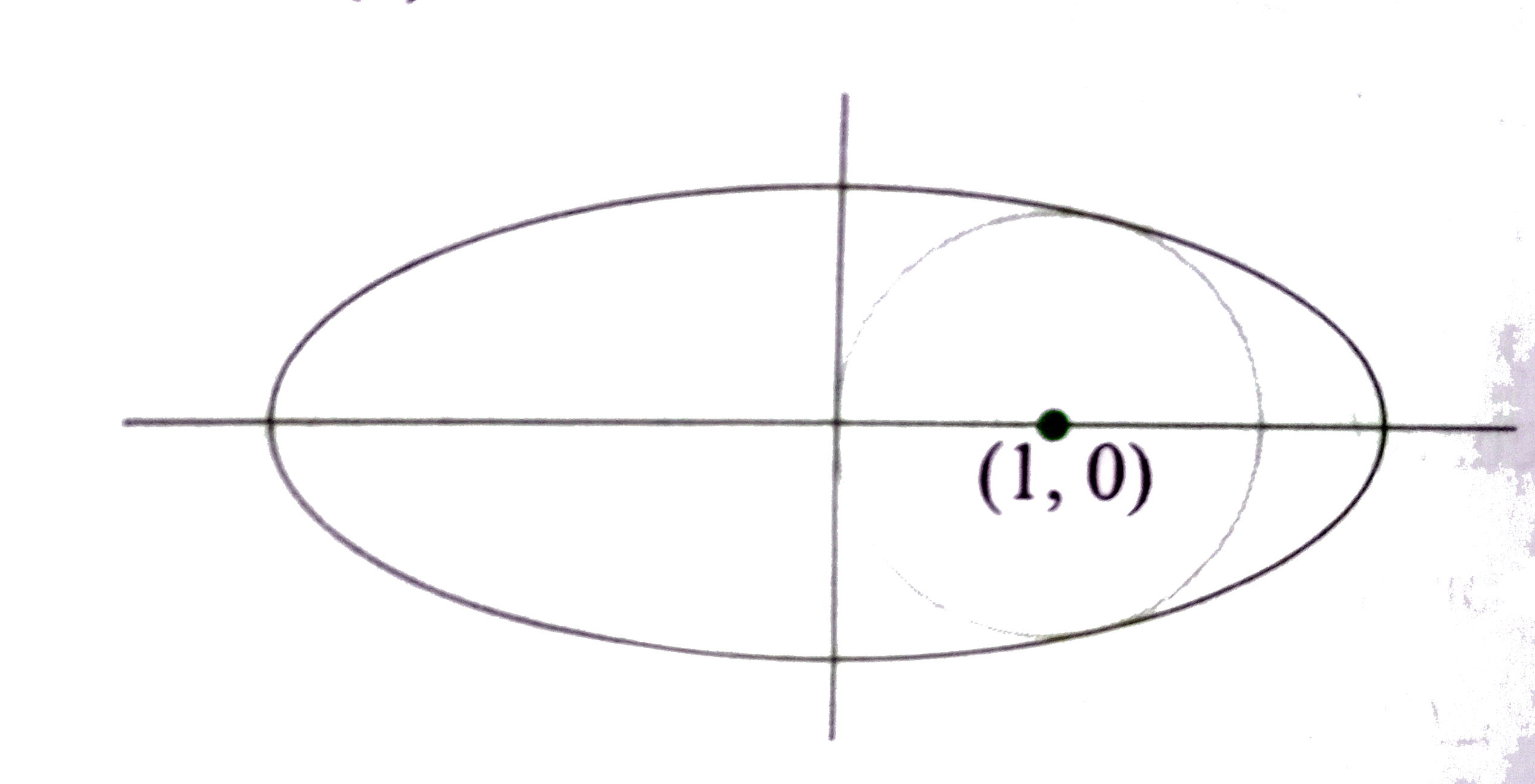
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is such that its has th...
Text Solution
|
- Consider an ellipse x^(2)/a^(2)+y^(2)/b^(2)=1 What is the length of ...
Text Solution
|
- The area of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is
Text Solution
|
- Determine the equation of the ellipse x^(2)/a^(2)+y^(2)/b^(2) = 1 suc...
Text Solution
|
- Find the length of Latus rectum of the ellipse (x^(2))/(a^(2))+(y^(2))...
Text Solution
|
- Ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 This is such that its area i...
Text Solution
|