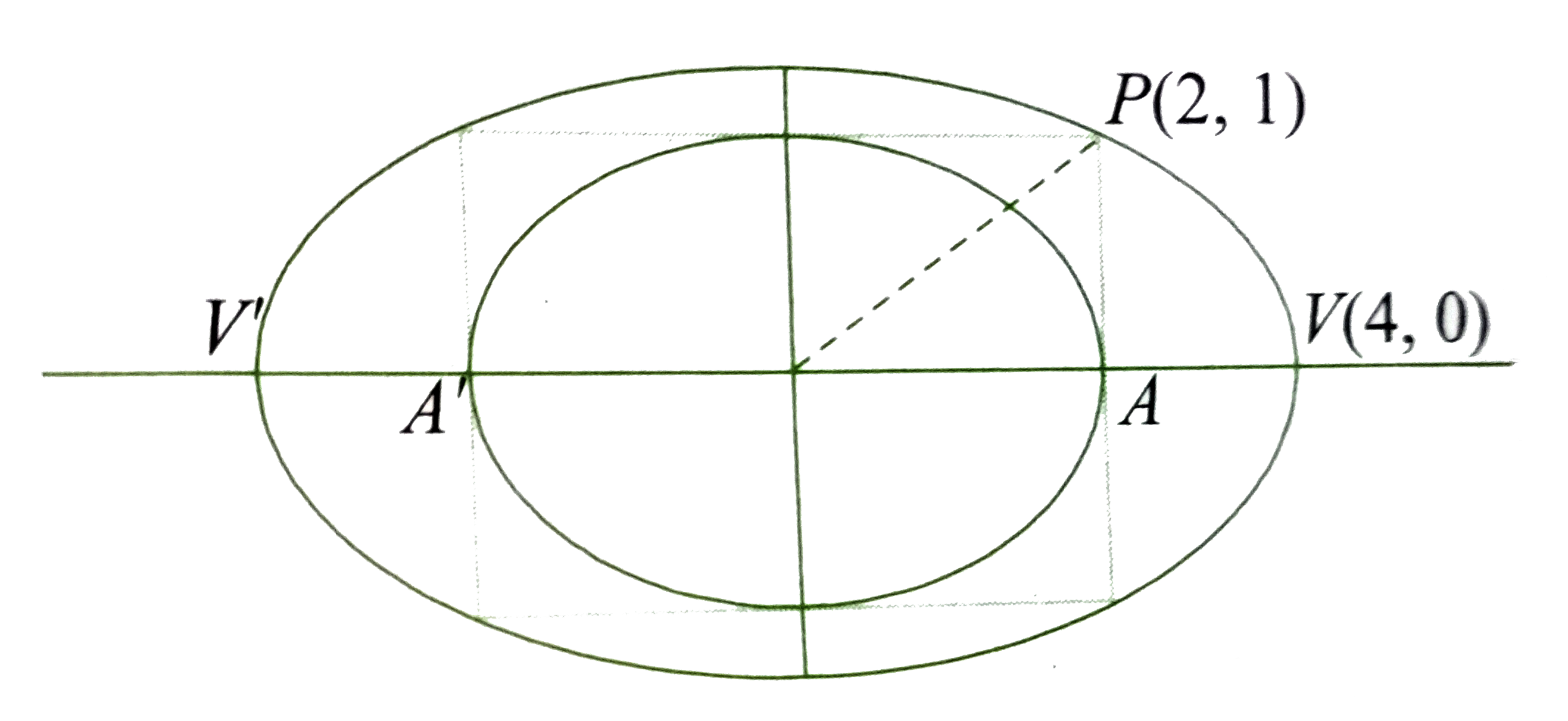
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ellipse x^(2)4y^(2)=4 is inscribed in a rectangle aligned with the...
Text Solution
|
- The ellipse x^2+""4y^2=""4 is inscribed in a rectangle aligned with th...
Text Solution
|
- If the major and minor axes of the ellipse are the axes of coordinates...
Text Solution
|
- Ellipse x^(2) + 4y^(2) = 4 is inscribed in a rectangle aligned with...
Text Solution
|
- The ellipse x^(2)+4y^(2)=4 is inscribed in a rectangle aligned with th...
Text Solution
|
- The ellipse E(1):(x^(2))/(9)+(y^(2))/(4)=1 is inscribed in a rectangle...
Text Solution
|
- Ellipse x^(2)+4y^(2)=4 Made in a rectangle which is inside another ell...
Text Solution
|
- The ellipse x^2+""4y^2=""4 is inscribed in a rectangle aligned with th...
Text Solution
|
- निर्देशी अक्षों के अनुदिश एक आयत के अन्तर्निहित (Inscribed) एक दीर्घवृ...
Text Solution
|