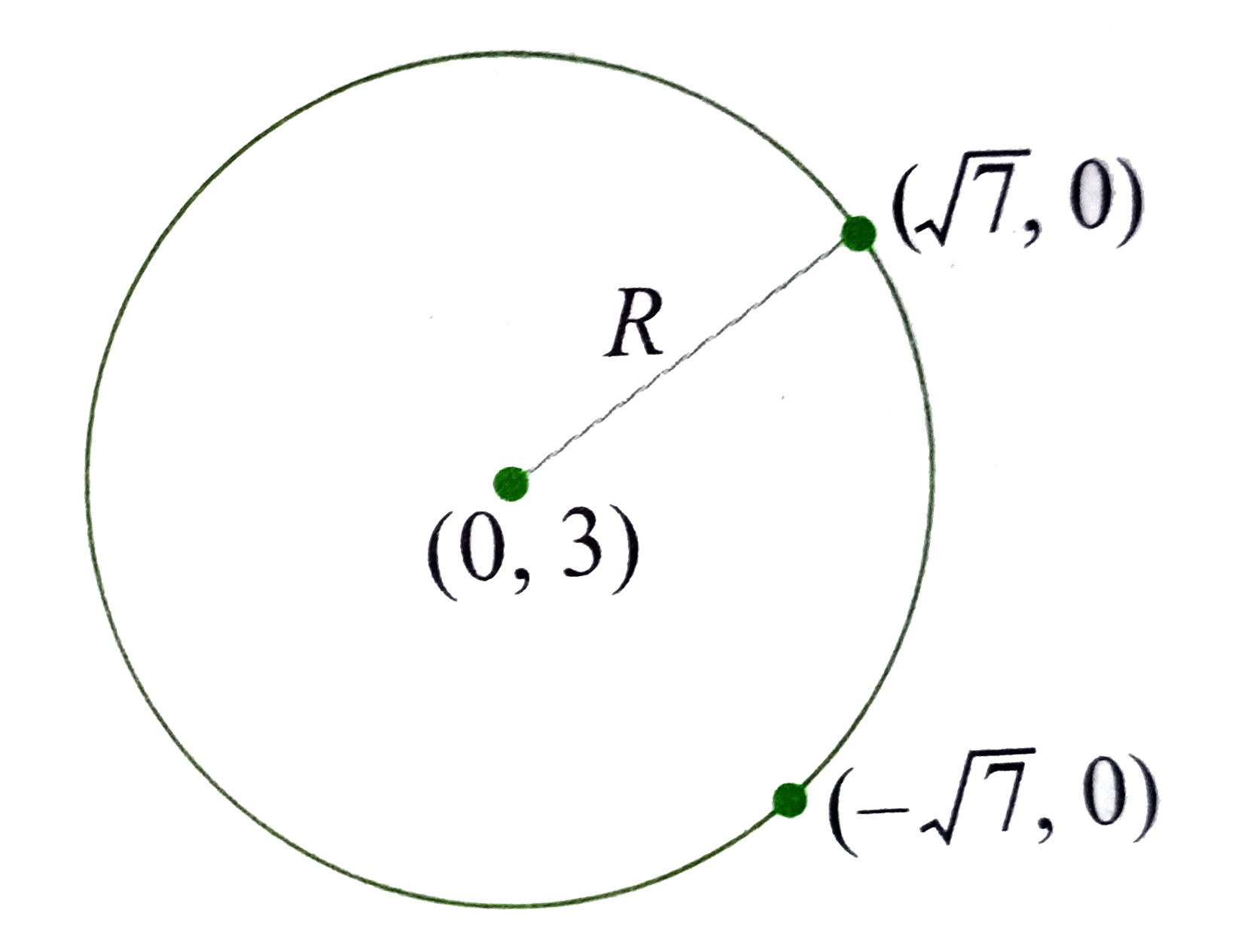
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The radius of the circle passing through the foci of the ellipse (x^2)...
Text Solution
|
- The radius of the circle passing through the foci of the ellipse (x^(2...
Text Solution
|
- the equilibrium of the circle passing through the foci of the el...
Text Solution
|
- The radius of the circle passing through the foci of (x^(2))/(16) + (y...
Text Solution
|
- The equation of the circle passing through the foci of the ellipse (x^...
Text Solution
|
- The equation of the circle passing through the foci of the ellipse x^(...
Text Solution
|
- The radius of the circle passing through the foci of the ellipse x^(2)...
Text Solution
|
- The radius of the circle passing throught the foci of the ellipse x^(2...
Text Solution
|
- The radius of the circle passing through the foci of the ellipse (x^2)...
Text Solution
|