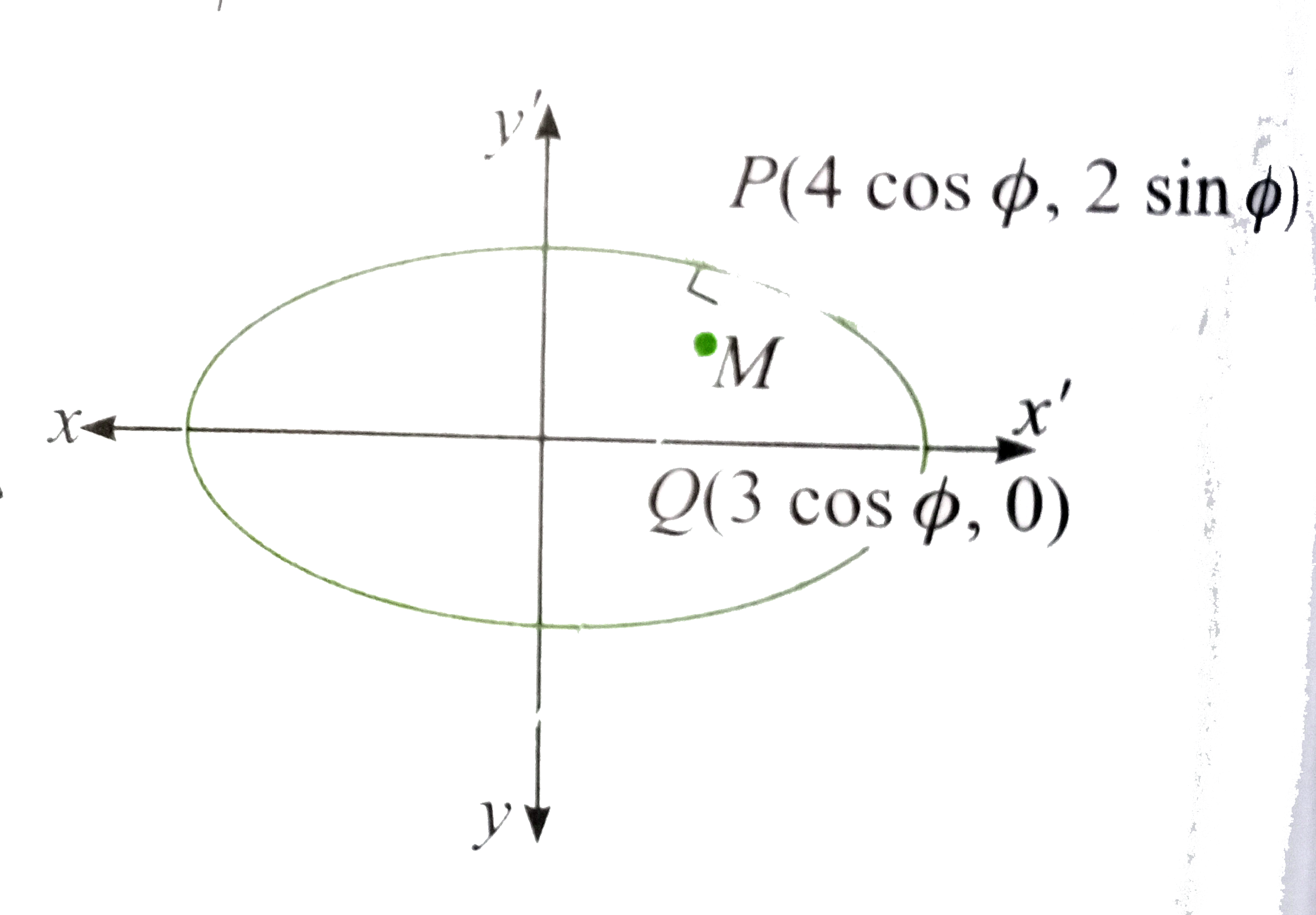
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The normal at a point P on the ellipse x^2+4y^2=16 meets the x-axis at...
Text Solution
|
- Rationales the denominator and simplify: (i)(sqrt(3)-sqrt(2))/(sqrt(3...
Text Solution
|
- The normal at a point P on the ellipse x^2+4y^2=16 meets the x-axis ...
Text Solution
|
- The distance of the point of contact from the origin of the line y=x-s...
Text Solution
|
- Simplify each of the following by rationalizing the denominator: I(I...
Text Solution
|
- If pair of tangents are drawn to the ellipse x^2/16 + y^2/9 = 1 from a...
Text Solution
|
- (3sqrt(7))/(sqrt(5)+sqrt(2))-(5sqrt(5))/(sqrt(2)+sqrt(7))+(2sqrt(2))/(...
Text Solution
|
- दीर्घवृत्त x^(2) + 4y^(2) = 16 के बिन्दु प पर खींचा गया अभिलम्ब x-अक्ष...
Text Solution
|
- The normal at a point P on the ellipse x^(2)+4y^(2)=16 meets the x-axi...
Text Solution
|