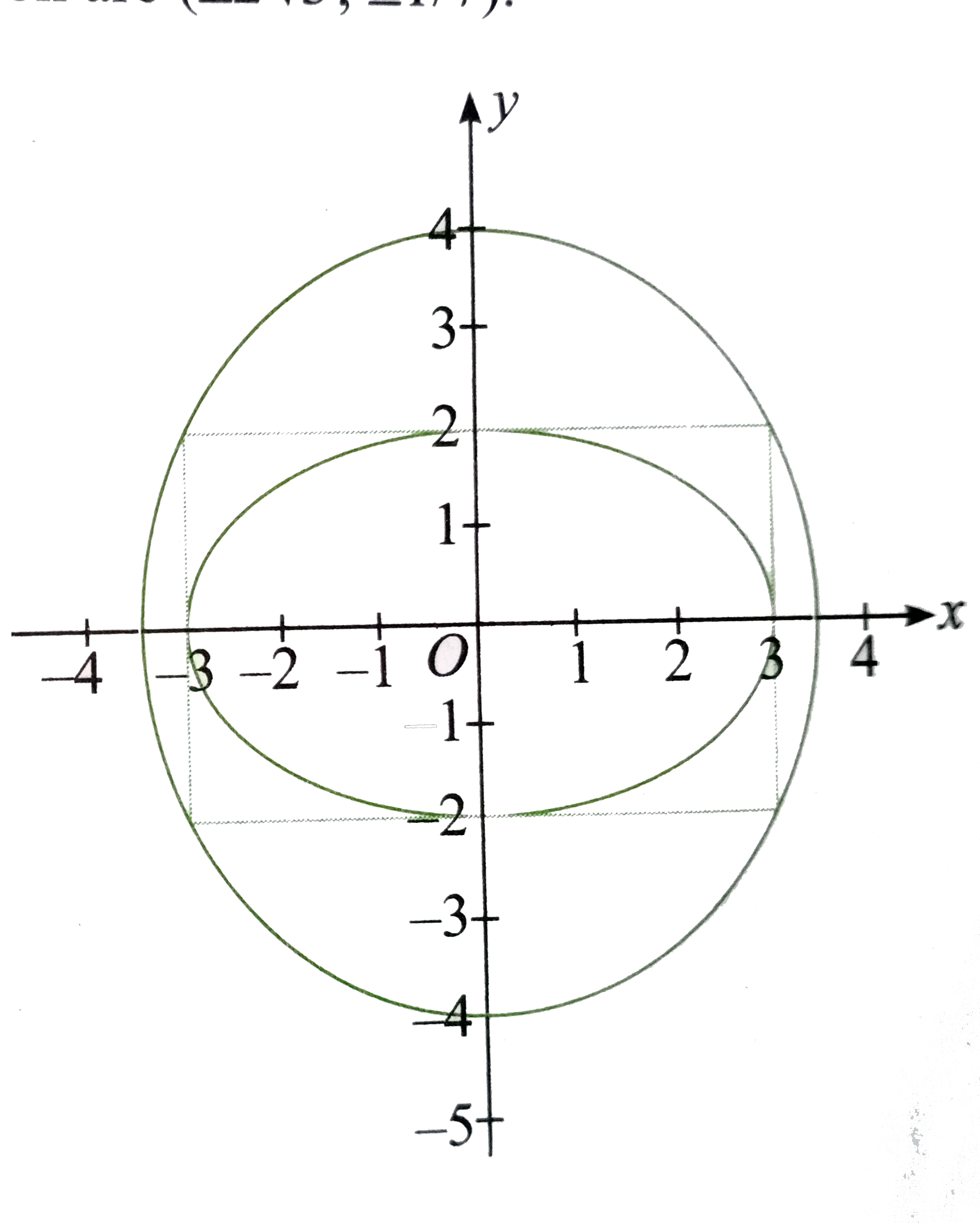
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ellipse E1:(x^2)/9+(y^2)/4=1 is inscribed in a rectangle R whose s...
Text Solution
|
- The ellipse E1:(x^2)/9+(y^2)/4=1 is inscribed in a rectangle R whose s...
Text Solution
|
- The ellipse E(1) : x^(2)/9 + y^(2)/4 =1 is inscribed in a rectangle ...
Text Solution
|
- Ellipse x^(2) + 4y^(2) = 4 is inscribed in a rectangle aligned with...
Text Solution
|
- The ellipse x^(2)+4y^(2)=4 is inscribed in a rectangle aligned with th...
Text Solution
|
- The ellipse E(1):(x^(2))/(9)+(y^(2))/(4)=1 is inscribed in a rectangle...
Text Solution
|
- நீள்வட்டம் E1 : frac{x^2}{9}+frac{y^2}{4}=1 செவ்வகம் R-க்குள் செவ்வகத்...
Text Solution
|
- The ellipse E1:(x^2)/9+(y^2)/4=1 is inscribed in a rectangle R whose s...
Text Solution
|
- दीर्घवृत E(1): x^2/9+y^2/4=1 आयत R के अन्तर्निहित है जिसकी भुजाये निर्...
Text Solution
|