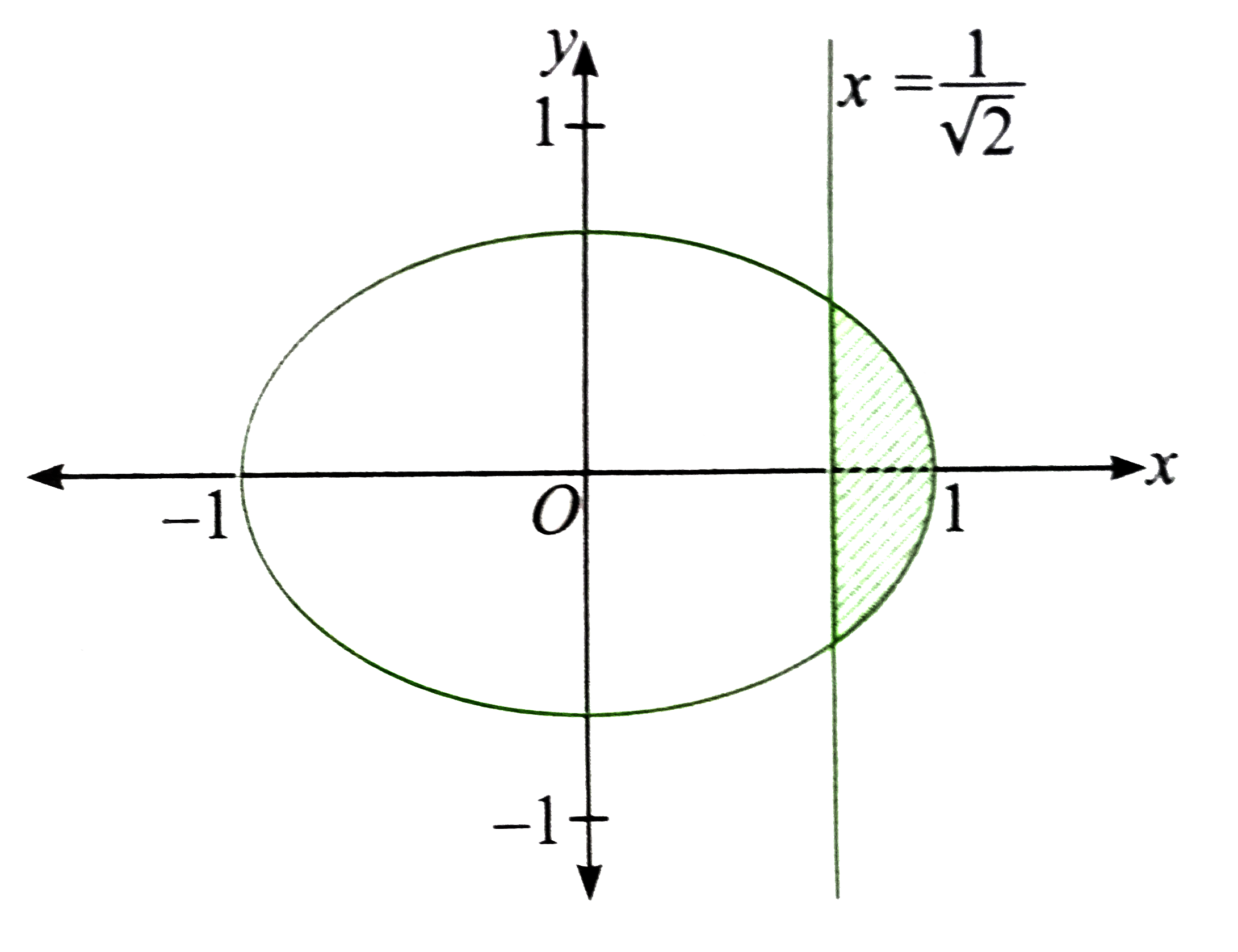
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider two straight lines, each of which is tangent to both the ci...
Text Solution
|
- Consider two straight lines, each of which is tangent to both the c...
Text Solution
|
- The line y = x intersects the hyperbola (x^(2))/(9) -(y^(2))/(25) = 1...
Text Solution
|
- Consider the parabola y^2 =4x and the ellipse 2x^2 + y^2 =6, intersect...
Text Solution
|
- An ellipse is drawn by taking a diameter of the circle (x – 1)^2 + y^2...
Text Solution
|
- If (0, 3+sqrt5) is a point on the ellipse whose foci and (2, 3) and (-...
Text Solution
|
- ऐसी दो सरल रेखाओं पर विचार कीजिए, जिनमें से प्रत्येक वृत्त x^(2)+y^(2)...
Text Solution
|
- If the circle whose diameter is the major axis of the ellipse (x^(2))/...
Text Solution
|
- Locus of the point of intersection of two perpendicular tangents to an...
Text Solution
|