Home
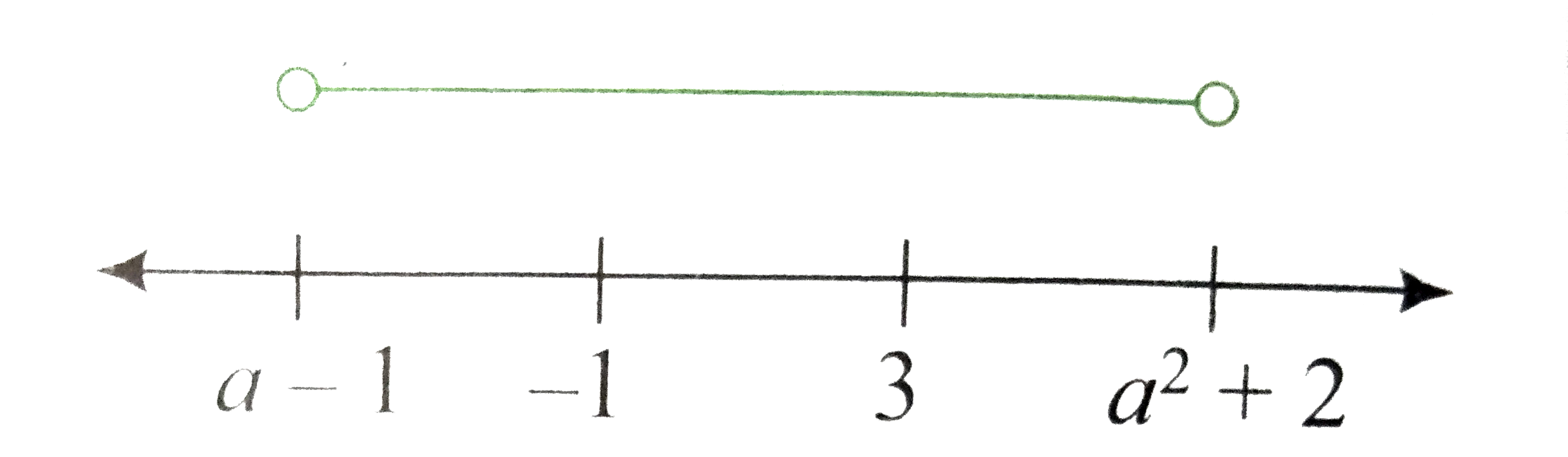
Class 12
MATHS
Find the set of all possible real value ...

Find the set of all possible real value of a such that the inequality `(x-(a-1))(x-(a^2+2))<0` holds for all `x in (-1,3)dot`

A

`(0, 1)`

B

`(infty, -2]`

C

`(-infty, - 1)`

D

`(1, infty)`

Text Solution

Verified by Experts

The correct Answer is:
2
We have,
` a - 1 le - 1 `
and ` a^(2) + 2 ge 3 `
`a le 0 and a^(2) ge 1`
Hence, a ` le - 1`
Promotional Banner

Topper's Solved these Questions

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise Multiple Correct Answer Type|38 Videos

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise Linked Comprechension Type|37 Videos

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 2.13|9 Videos

  • STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise ARCHIVES (NUMERICAL VALUE TYPE)|1 Videos

  • THREE DIMENSIONAL GEOMETRY

    CENGAGE PUBLICATION|Exercise All Questions|291 Videos

Similar Questions

Explore conceptually related problems

The set of all possible real values of a such that the inequality (x-(a-1))(x-(a^2-1))<0 holds for all x in (-1,3) is a. (0,1) b. (oo,-1] c. (-oo,-1) d. (1,oo)

Find all possible values of sqrt(|x|-2)

Find all possible values of (x^2+1)/(x^2-2) .

Find all the possible values of 1/x for x>3 .

let f(x)=-x^3+(b^3-b^2+b-1)/(b^2+3b+2) if x is 0 to 1 and f(x)=2x-3 if x is 1 to 3 .All possible real values of b such that f (x) has the smallest value at x=1 are

Let S be the set of all non-zero real numbers alpha such that the quadratic equation alphax^2-x+alpha=0 has two distinct real roots x_1 and x_2 satisfying the inequality abs(x_1-x_2)lt1 . Which of the following intervals is (are) a subset(s) of S ?

For x in R , find all possible values of (i)|x-4|-6

The sum pf all real values of x satisfying the equation (x^(2)-5x+5)^(x^(2)-4x-60)=1 is

The set of values of x which satisfy the inequation (5x+8)/(4-x)lt2 , are-

Find the values of x which satisfy the inequality -3 lt 2x -1 lt 19 .

CENGAGE PUBLICATION-THEORY OF EQUATIONS-Single Correct Answer Type : Exercise
  1. The set of value of a for which (a-1)x^2(a+1)x+a-1geq0 is true for all...

    Text Solution

    |

  2. If the equation a x^2+b x+c=x has no real roots, then the equation a(a...

    Text Solution

    |

  3. If a x 62+b x+c=0 has imaginary roots and a-b+c >0 then the set of poi...

    Text Solution

    |

  4. Given x, y in R , x^(2) + y^(2) gt 0 . Then the range of (x^(2) + ...

    Text Solution

    |

  5. x1 and x2 are the roots of a x^2+b x+c=0 and x1x2<0. Roots of x1(x-x2)...

    Text Solution

    |

  6. If a ,b ,c ,d are four consecutive terms of an increasing A.P., then t...

    Text Solution

    |

  7. If roots of x^2-(a-3)x+a=0 are such that at least one of them is great...

    Text Solution

    |

  8. All the values of m for which both roots of the equation x^(2)-2mx+m^(...

    Text Solution

    |

  9. if the roots of the quadratic equation (4p - p^(2) - 5)x^(2) - 2mx ...

    Text Solution

    |

  10. The interval of a for which the equation t a n^2x-(a-4)tanx+4-2a=0 has...

    Text Solution

    |

  11. The range of a for which the equation x^2+x-4=0 has its smaller root i...

    Text Solution

    |

  12. Find the set of all possible real value of a such that the inequality ...

    Text Solution

    |

  13. If the equation cof^4x-2cos e c^2x+a^2=0 has at least one solution, th...

    Text Solution

    |

  14. If a ,b ,c are distinct positive numbers, then the nature of roots of ...

    Text Solution

    |

  15. For x^2-(a+3)|x|+4=0 to have real solutions, the range of a is a. (-oo...

    Text Solution

    |

  16. If the quadratic equation4x^2-2(a+c-1)x+a c-b=0(a > b > c) Both roots...

    Text Solution

    |

  17. If the equaion x^(2) + ax+ b = 0 has distinct real roots and x^(2) + a...

    Text Solution

    |

  18. The equation 2^(2x) + (a - 1)2^(x+1) + a = 0 has roots of opposit...

    Text Solution

    |

  19. All the values of ' a ' for which the quadratic expression a x^2+(a-2)...

    Text Solution

    |

  20. If a0, a1, a2, a3 are all the positive, then 4a0x^3+3a1x^2+2a2x+a3=0 h...

    Text Solution

    |