Text Solution
Verified by Experts
Topper's Solved these Questions
SETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise For Session 1|11 VideosSETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise For Session 2|10 VideosSEQUENCES AND SERIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|38 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)|1 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-SETS, RELATIONS AND FUNCTIONS -Exercise (Questions Asked In Previous 13 Years Exam)
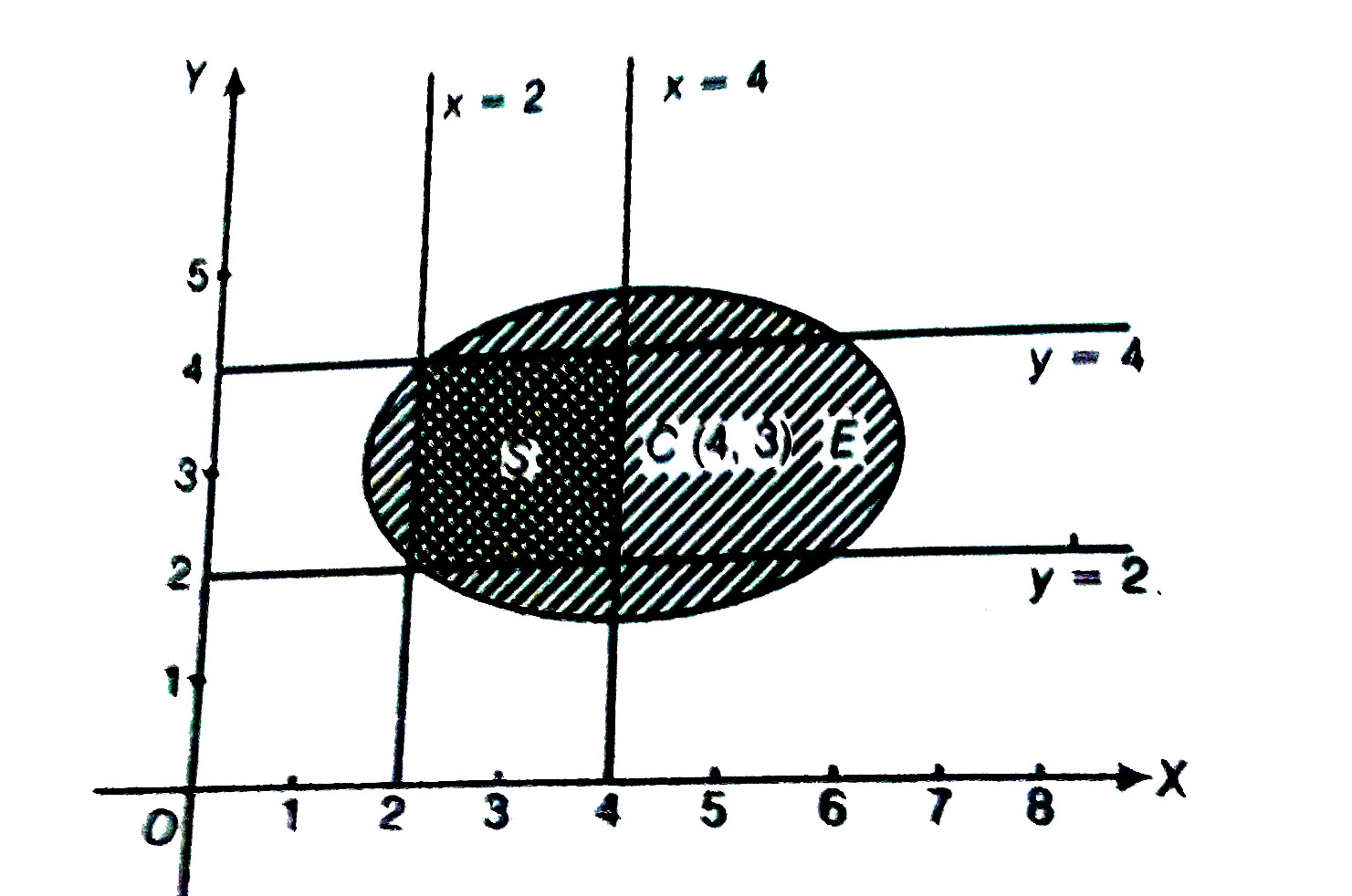
- The sets S and E are defined as given below: S={(x,y): |x-3|lt1and|y...
Text Solution
|
- Let R = {(3, 3), (6, 6), (9, 9), (6, 12), (3, 9), (3, 12),(12,12), (3,...
Text Solution
|
- Let w denote the words in the english dictionary. Define the relation ...
Text Solution
|
- N is the set of natural numbers. The relation R is defined on NxxN as ...
Text Solution
|
- If A, B and C are three sets such that AnnB""=""AnnC and AuuB""=""AuuC...
Text Solution
|
- Two finite sets have m and n elements. The total number of subsets of ...
Text Solution
|
- Consider the following relations: R = {(x, y) | x, y are real numbers ...
Text Solution
|
- Let P={theta:sintheta-costheta=sqrt2costheta}and Q={theta: sintheta+co...
Text Solution
|
- Find the value of x when tanx=1.
Text Solution
|
- Evaluate inttan^2x dx
Text Solution
|
- If A and B two sets containing 2 elements and 4 elements, respectively...
Text Solution
|
- If X={4^(n)-3n-1:ninN}andy={9(n-1):ninN}, then X uu Y equals a. X b. ...
Text Solution
|
- Let A and B be too sets containing four and two elements respectively ...
Text Solution
|