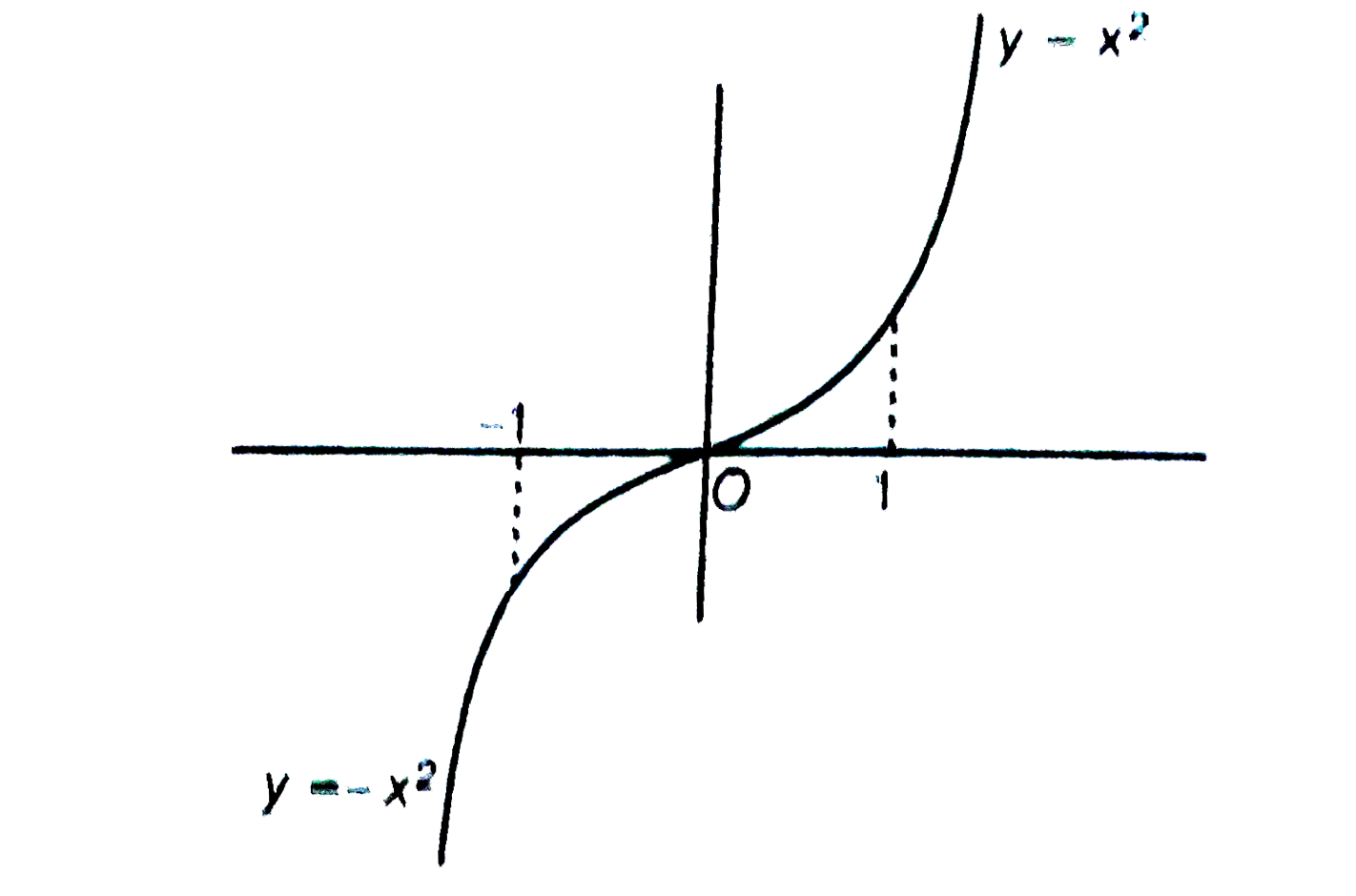
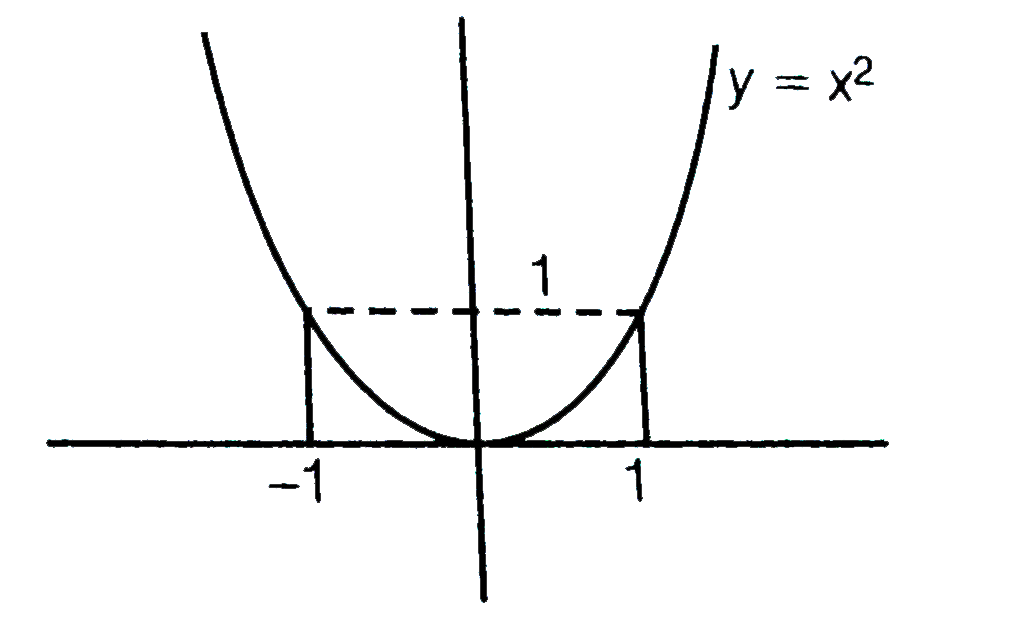
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|12 VideosSETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise (Statement I And Ii Type Questions)|4 VideosSEQUENCES AND SERIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|38 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)|1 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-SETS, RELATIONS AND FUNCTIONS -Exercise (Subjective Type Questions)
- If A = {x : x is a natural number}, B = {x : x is an even natural numb...
Text Solution
|
- let U= {1,2,3,4,5,6,7,8} A = {1,2,,3,4} then find the A complement
Text Solution
|
- If A = {x : x is a natural number }, B = {x : x is an even natural num...
Text Solution
|
- In a group of children, 35 play football out of which 20 play football...
Text Solution
|
- Of the members of three athletic teams in a certain school, 21 are in ...
Text Solution
|
- In a survey of 200 students of a school, it was found that 120 study...
Text Solution
|
- In a survey of population of 450 people, it is found that 205 can spea...
Text Solution
|
- A group of 123 workers went to a canteen for cold drinks, ice-cream an...
Text Solution
|
- Let n be a fixed positive integer. Define a relation R on Z as follows...
Text Solution
|
- Show that if A= { 1,2,3} and R ={(1,1),(2,2),(3,3) (1,2),(2,1),(2,3),...
Text Solution
|
- The given relation is defined on the set of real numbers. a R b iff |a...
Text Solution
|
- Let A = {x: -1lexle1} = B for each of the following functions from A t...
Text Solution
|
- If the functions f and g defined from the set of real number R to R su...
Text Solution
|
- If f(x)=(x^(2)-x)/(x^(2)+2x), then find the domain and range of f. Sho...
Text Solution
|
- If the functions f, g and h are defined from the set of real numbers R...
Text Solution
|