Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)
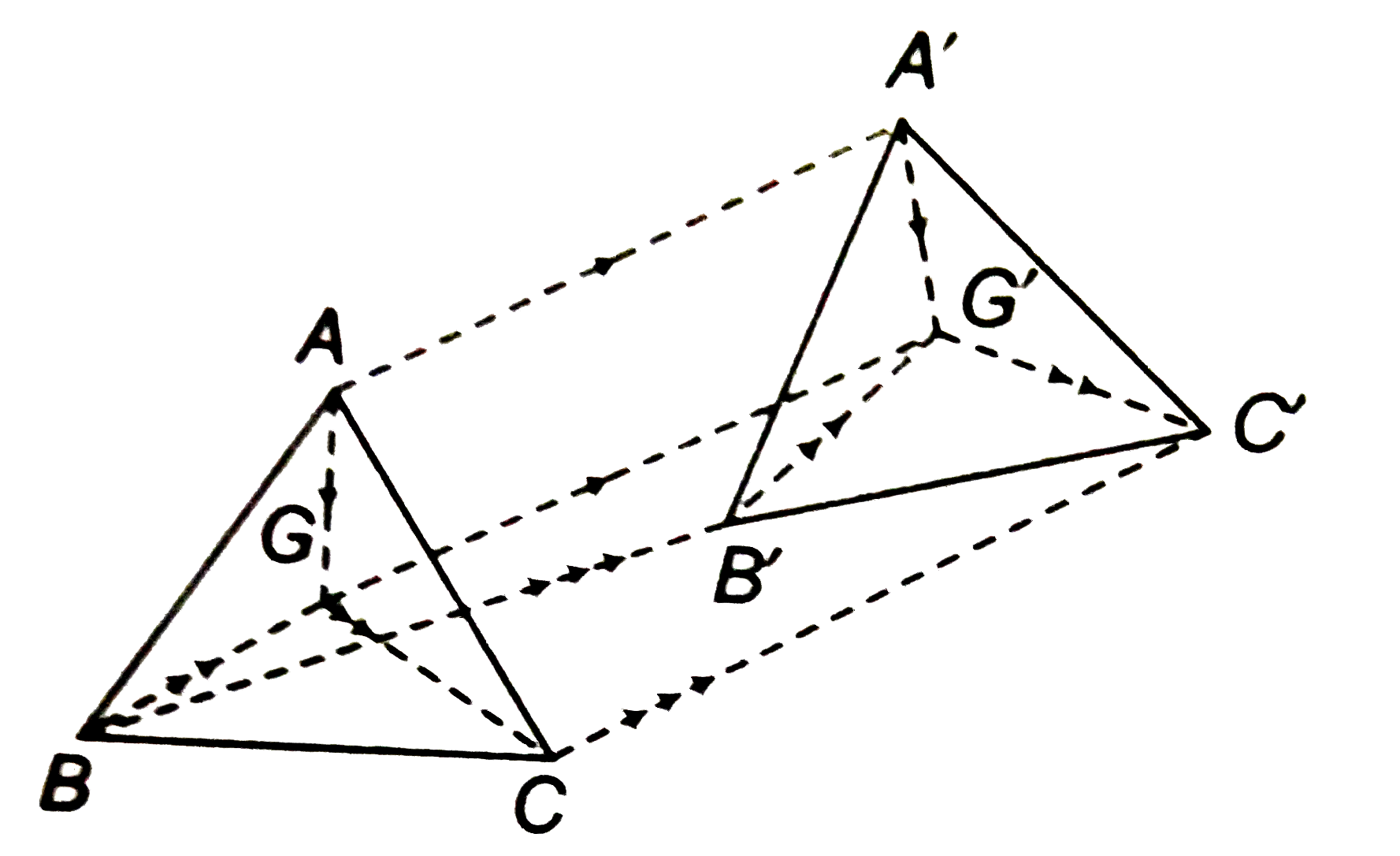
- If G is the centroid of Delta ABC and G' is the centroid of Delta A'...
Text Solution
|
- If vectors vec(AB) = -3hati+ 4hatk and vec(AC) = 5hati -2hatj+4hatk ar...
Text Solution
|
- Let a,b and c be three non-zero vectors which are pairwise non-colline...
Text Solution
|
- The non-zero vectors a,b and c are related by a=8b and c=-7b angle bet...
Text Solution
|
- If C is the middle point of AB and P is any point outside AB, then
Text Solution
|
- Let a,b and c be three non-zero vectors such that no two of these are ...
Text Solution
|
- If veca, vecb and vecc are non-coplanar vectors and lamda is a real nu...
Text Solution
|
- Area of a rectangle having vertices A, B, C and D with position vector...
Text Solution
|
- If a,b, and c are all different and if |{:(a,a^(2),1+a^(3)),(b,b^(2...
Text Solution
|
- The vector hat i+x hat j+3 hat k is rotated through an angle theta an...
Text Solution
|