Home
Class 12
MATHS
In a regular hexagon ABCDEF, prove that ...

In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.

Text Solution

Verified by Experts

The correct Answer is:
B
By triangle law, `AB=AD-BD,AC=AD-CD`

Therefore, `AB+AC+AD+AE+AF`
`=3AD+(AE-BD)+(AF-CD)=3AD`
hence, `lamda=3" "(becauseAE=BD,AF=CD)`
Promotional Banner

Topper's Solved these Questions

  • VECTOR ALGEBRA

    ARIHANT MATHS|Exercise VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions|1 Videos

  • VECTOR ALGEBRA

    ARIHANT MATHS|Exercise Exercise (More Than One Correct Option Type Questions)|7 Videos

  • VECTOR ALGEBRA

    ARIHANT MATHS|Exercise Exercise For Session 3|11 Videos

  • TRIGONOMETRIC FUNCTIONS AND IDENTITIES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|18 Videos

Similar Questions

Explore conceptually related problems

If ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB .

In a regular hexagon ABCDEF, bar(AB) + bar(AC)+bar(AD)+ bar(AE) + bar(AF)=k bar(AD) then k is equal to

In any triangle ABC, prove that AB^2 + AC^2 = 2(AD^2 + BD^2) , where D is the midpoint of BC.

In a regular hexagon ABCDEF, AB=a,BC=b and CD=c. Then, vec(AE) is equal to

Consider the regular hexagon ABCDEF with centre at O (origin). Q. Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is

Five point charges, each having a charge q are placed on the five croners A,B,C, D and E of a regular hexagon ABCDEF having each side of length a. Find the electric field at the centre of the hexagon.

ABCDEF is a regular hexagon. Express the vectors vec (CD) , vec (DE) , vec (EF) , vec (FA) , vec (CE) in terms of vec (AB) and vec (BC) .

In Fig. , AB > AC , show that AB > AD .

In Fig. , AB > AC , show that AB > AD .

In the Fig. If AB = AD . Prove that AB > CD .

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Single Option Correct Type Questions)
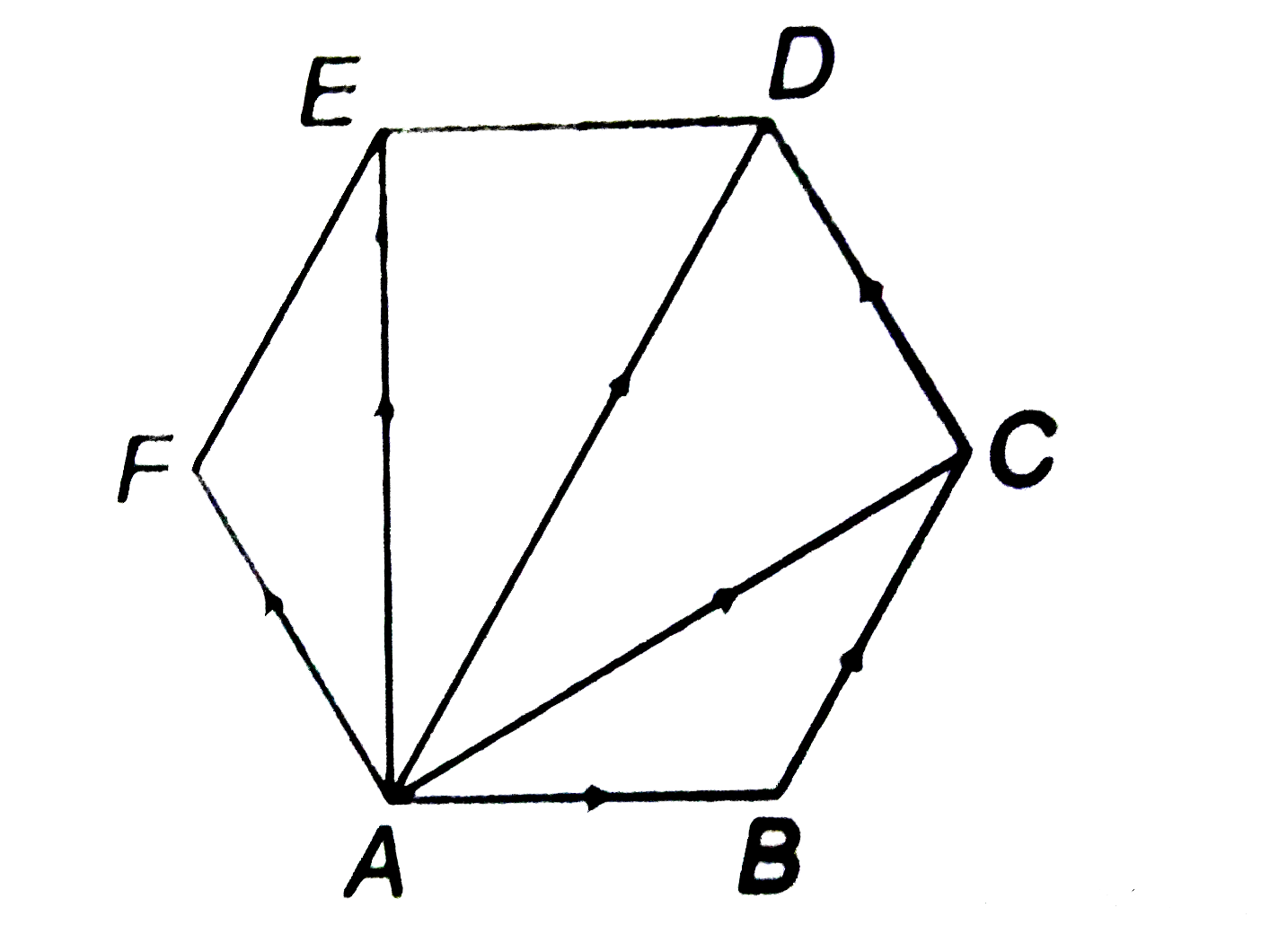
  1. If ABCDEF is a regular hexagon then vec(AD)+vec(EB)+vec(FC) equals :

    Text Solution

    |

  2. Find the discriminant of the quadratic equation x^2+3x+2

    Text Solution

    |

  3. In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.

    Text Solution

    |

  4. Find the dot product of the vector 2hati+3hatj+1hatk and 1hati+2hatj+3...

    Text Solution

    |

  5. If a and b are two non-zero and non-collinear vectors then a+b and a-b...

    Text Solution

    |

  6. If |veca+ vecb| lt | veca- vecb|, then the angle between veca and vecb...

    Text Solution

    |

  7. The magnitudes of mutually perpendicular forces a,b and c are 2,10 and...

    Text Solution

    |

  8. If hati-3hatj+5hatk bisects the angle between hata and -hati+2hatj+2ha...

    Text Solution

    |

  9. Find the discriminant of the quadratic equation x^2+5x+4=0 and also fi...

    Text Solution

    |

  10. Given three vectors vec a=6 hat i-3 hat j , vec b=2 hat i-6 hat ja ...

    Text Solution

    |

  11. ' I ' is the incentre of triangle A B C whose corresponding sides are ...

    Text Solution

    |

  12. If vecx and vecy are two non-collinear vectors and ABC is a triangle w...

    Text Solution

    |

  13. If vec xa n d vec y are two non-collinear vectors and a, b, and c r...

    Text Solution

    |

  14. If the resultant of two forces is equal in magnitude to one of the ...

    Text Solution

    |

  15. If vec b is a vector whose initial point divides the join of 5 hat ...

    Text Solution

    |

  16. find the term independent of x in the expansion of (2x-1/x)^2 ?

    Text Solution

    |

  17. If veca and vecb are two unit vectors and theta is the angle between t...

    Text Solution

    |

  18. A, B, C and D have position vectors veca, vecb, vecc and vecd, repecti...

    Text Solution

    |

  19. if alpha and beta are the root of the quadratic polynomial f(x) = x^2-...

    Text Solution

    |

  20. If a +b+c = alphad, b+c+d=beta a and a, b, c are non-coplanar, then t...

    Text Solution

    |