Text Solution
Verified by Experts
Topper's Solved these Questions
MATRICES
ARIHANT MATHS|Exercise Exercise For Session 1|9 VideosMATRICES
ARIHANT MATHS|Exercise Exercise For Session 2|19 VideosMATHEMATICAL INDUCTION
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|2 VideosMONOTONICITY MAXIMA AND MINIMA
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|31 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-MATRICES -Exercise (Questions Asked In Previous 13 Years Exam)
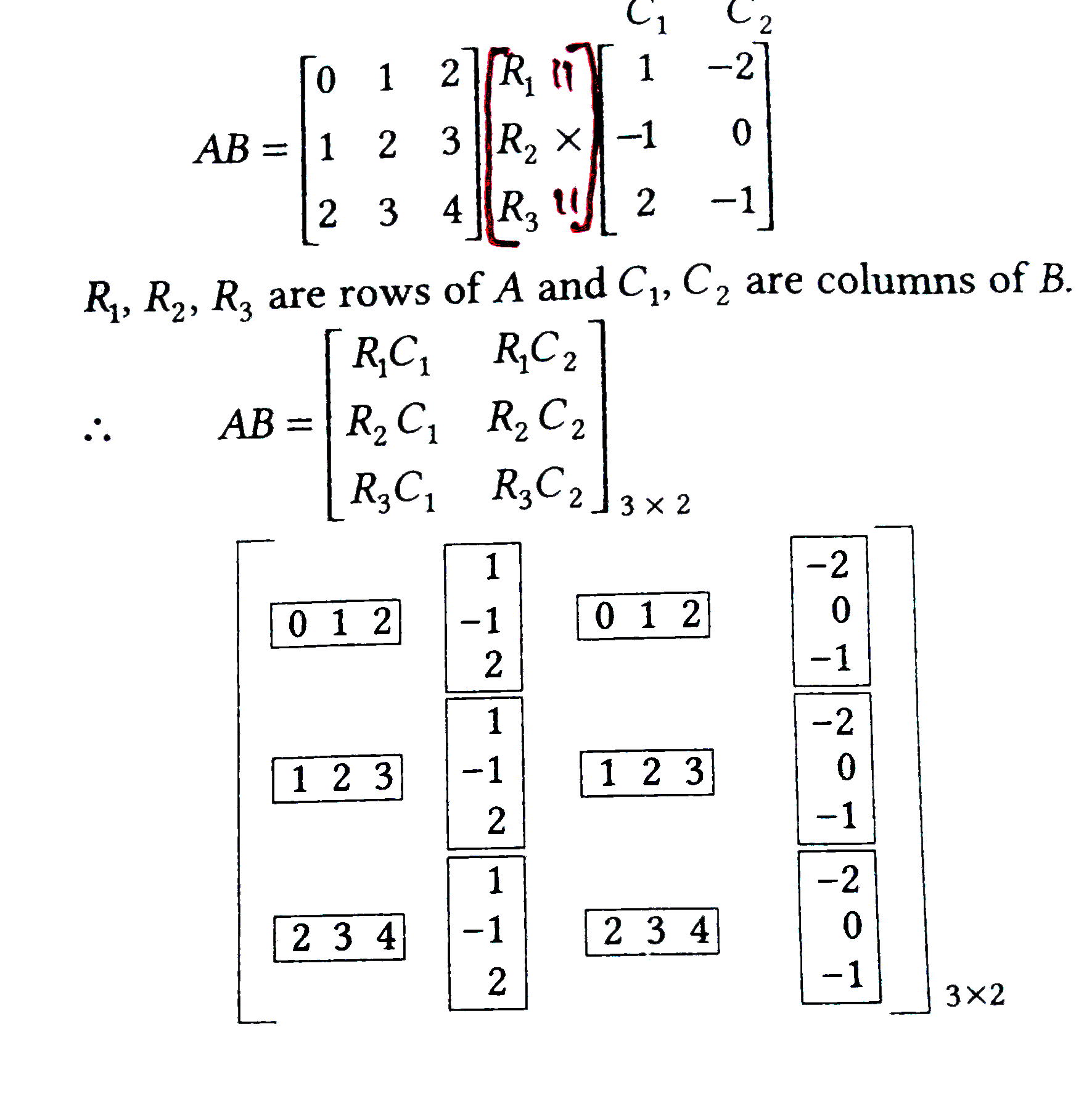
- If A = [{:(0,1,2),(1,2,3),(2,3,4):}] and B=[{:(1,-2),(-1,0),(2,-1):}] ...
Text Solution
|
- Let A=[(1,0,0),(0,1,1),(0,-2,4)],I=[(1,0,0),(0,1,0),(0,0,1)] and A^-1=...
Text Solution
|
- Evluate int 3x^2 dx
Text Solution
|
- If A=[(1,0),(1,1)] and I=[(1,0),(0,1)] then which one of the following...
Text Solution
|
- If A^(2)-A+I=O, then A^(-1) is equal to
Text Solution
|
- Let {:A=[(1,0,0),(2,1,0),(3,2,1)]:}and U1,U2,U3 be column matrices sat...
Text Solution
|
- Let A = [(1,0,0), (2,1,0), (3,2,1)], and U1, U2 and U3 are columns of ...
Text Solution
|
- If A= ((1,0,0),(2,1,0),(3,2,1)), U(1), U(2), and U(3) are column matri...
Text Solution
|
- Let A=[{:(1,2),(3,4):}]and B = [{:(a,0),(0,b):}] where a, b are natura...
Text Solution
|
- If A and B are square matrices of size nxxn such that A^2-B^2 = (A-B)(...
Text Solution
|
- Let A= [[5,5alpha,alpha],[0,alpha,5alpha],[0,0,5]] . If |A^2|...
Text Solution
|
- Let A and B be 3xx3 matrtices of real numbers, where A is symmetric, "...
Text Solution
|
- Let A be a square matrix all of whose entries are integers. Then wh...
Text Solution
|
- Let A be a 2xx2 matrix with real entries. Let I be the 2xx2 identi...
Text Solution
|
- Let A be the set of all 3xx3 symmetric matrices all of whose either 0 ...
Text Solution
|
- Let A be the set of all 3xx3 symmetric matrices all of whose either 0 ...
Text Solution
|
- The number of 3xx3 matrices A whose are ether 0 or 1 and for which t...
Text Solution
|
- Let A be a 2xx2 matrix Statement -1 adj (adjA)=A Statement-2 abs(a...
Text Solution
|
- The number of 3xx3 matrices a whose entries are either 0 or 1 and for ...
Text Solution
|
- Let P be an odd prime number and T(p) be the following set of 2xx2 mat...
Text Solution
|
- Let p be an odd prime number and T(P) be the following set of 2xx2 m...
Text Solution
|