Home
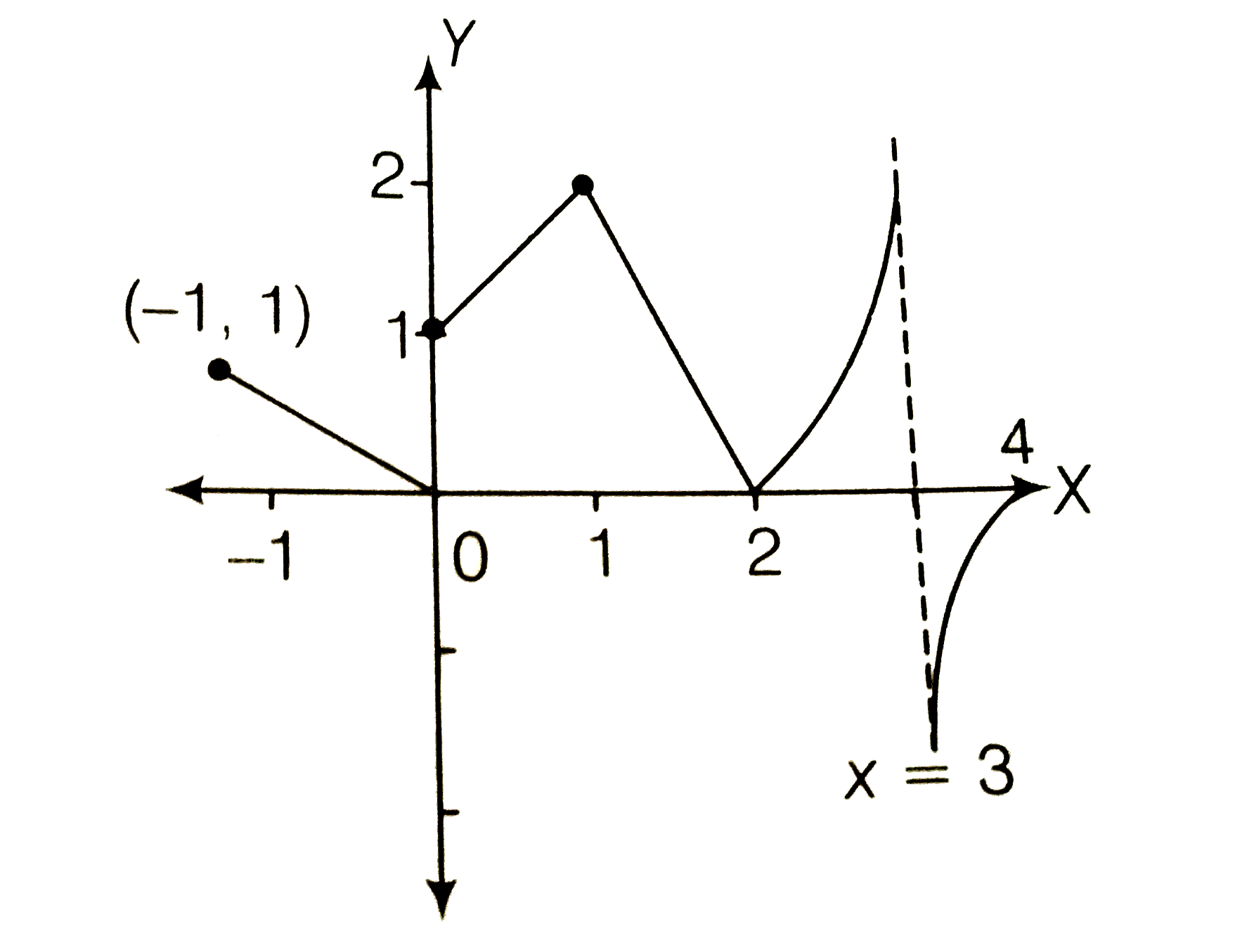
Class 12
MATHS
The graph of the function y=f(x) is show...

The graph of the function `y=f(x)` is shown in the adjacent figure then correct statement is

A

`lim_(xto0^(+))f(x)=1`

B

`lim_(xto1)f(x)=2`

C

`lim_(xto3)f(x)=` does not exist

D

`lim_(xto4)f(x)=0`

Text Solution

Verified by Experts

The correct Answer is:
A, B, C, D
Promotional Banner

Topper's Solved these Questions

  • LIMITS

    ARIHANT MATHS|Exercise Exercise (Passage Based Questions)|10 Videos

  • LIMITS

    ARIHANT MATHS|Exercise Exercise (Matching Type Questions)|3 Videos

  • LIMITS

    ARIHANT MATHS|Exercise Exercise (Single Option Correct Type Questions)|38 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|8 Videos

  • LOGARITHM AND THEIR PROPERTIES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 Videos

Similar Questions

Explore conceptually related problems

The graph of the function y = f(x) is symmetrical about the line x = 2, then:

The graph of the function y=f(x) passing through the point (0,1) and satisfying the differential equation (dy)/(dx)+ycosx=cosx is such that

Draw the graph of the following function. 2f(x)

Draw the graph of the following function. -f(x)

Draw the graph of the following function. f(-x)

The graph of the function y=f(x) has a unique tangent at the point (a,0) through the graph passes. Then, "lim"_(xrarra)[["log"_(e) (1+6) f (x)]]/(3f (x)) is equal to :

Draw the graph of the following function. f(x+1)

Draw the graph of the function f(X) = x^2 and show that it is not invertible. Restrict its domain suitably so that f^-1 may exist, find f^-1 and draw its graph.

Sketch the graphs of the following function : y=2 sin x .

Sketch the graphs of the following function : y = sin^2 x .