A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LIMITS
ARIHANT MATHS|Exercise Exercise (Matching Type Questions)|3 VideosLIMITS
ARIHANT MATHS|Exercise MATCHING TYPE QUESTIONS|1 VideosLIMITS
ARIHANT MATHS|Exercise Exercise (More Than One Correct Option Type Questions)|15 VideosINVERSE TRIGONOMETRIC FUNCTIONS
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|8 VideosLOGARITHM AND THEIR PROPERTIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-LIMITS-Exercise (Passage Based Questions)
- If lim(xtoa)f(x)=1 and lim(xtoa)g(x)=oo then lim(xtoa){f(x)}^(g(x))=e^...
Text Solution
|
- If lim(xtoa)f(x)=1 and lim(xtoa)g(x)=oo then lim(xtoa){f(x)}^(g(x))=e^...
Text Solution
|
- If lim(xtoa)f(x)=1 and lim(xtoa)g(x)=oo then lim(xtoa){f(x)}^(g(x))=e^...
Text Solution
|
- Find dy/dx if 2x-3y=tanx
Text Solution
|
- Find |A| If A = |(x^2, 2x), (x^4 , 5x)|
Text Solution
|
- Let f(x)=lim(ntooo)(cos sqrt(x/n))^(n),g(x)=lim(nto oo)(1+x+x root(n)(...
Text Solution
|
- How many 4 digits numbers can be formed from the digits 1 to 9 if not ...
Text Solution
|
- Find dy/dx if 2y=e^y-2x
Text Solution
|
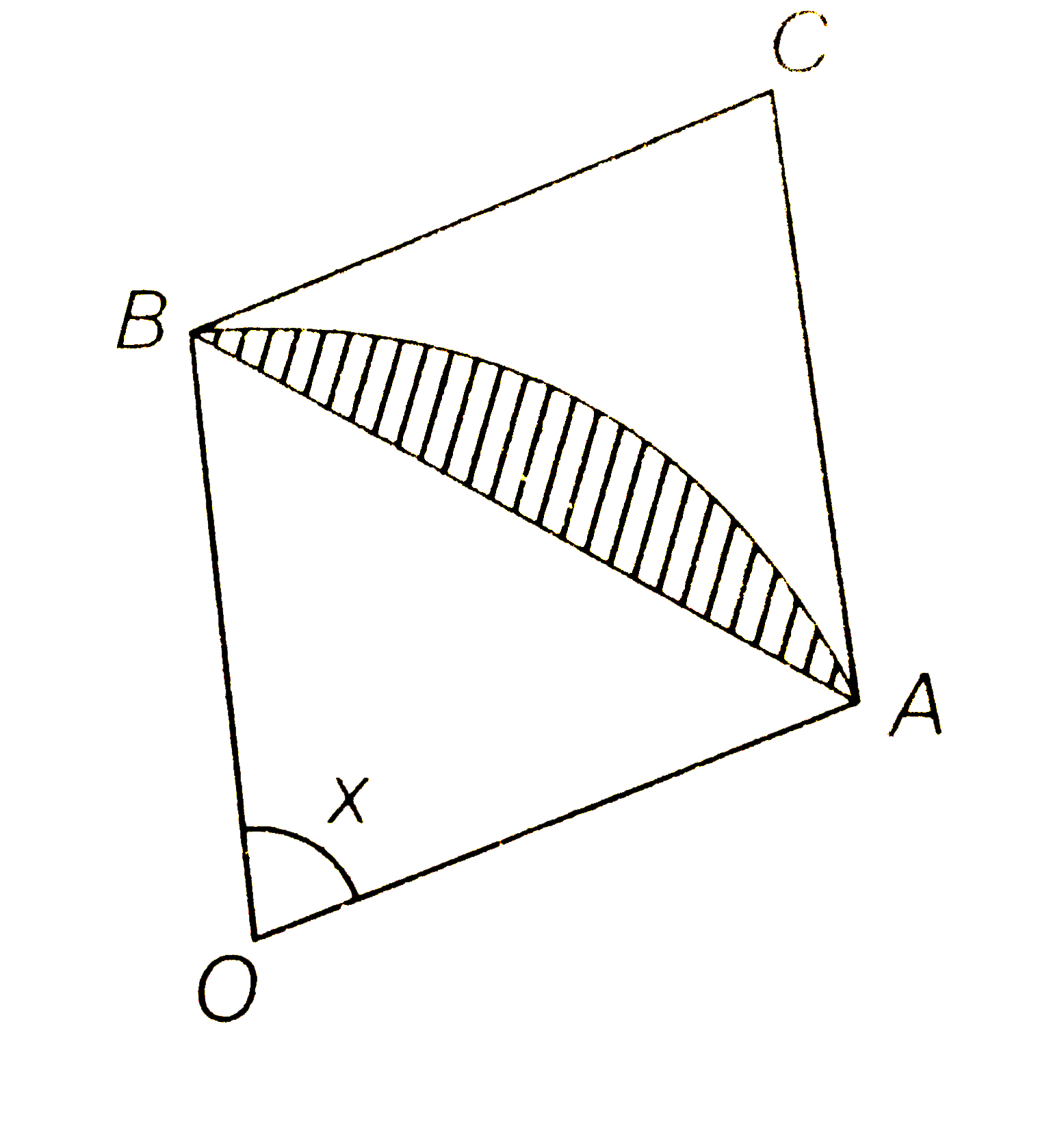
- A circle arc of radius 1 subtends an angle of x radians as shown in fi...
Text Solution
|
- A circle arc of radius 1 subtends an angle of x radians as shown in fi...
Text Solution
|