A
B
C
D
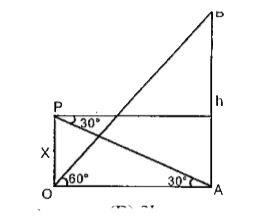
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A tower subtends an angle of 30^(@) at a point on the same level as it...
Text Solution
|
- A tower subtends an angle of 30^(@) at a point on the same level as it...
Text Solution
|
- A tower subtends an angle of 30^(@) at a point on the same level as th...
Text Solution
|
- A tower subtends and angle 60^(@) at a point A in the plane of its bas...
Text Solution
|
- A tower subtends an angle of 60^(@) at a point on the plane passing th...
Text Solution
|
- A tower subtends an angle of 30^@ at a point on the same level as the ...
Text Solution
|
- The electric pole subtends an angle of 30^(@) at a point on the same l...
Text Solution
|
- A tower subtends an angle of 60^(@) at a point on the same level as th...
Text Solution
|
- A vertical tower subtends an angle of 60^(@) at a point on the same le...
Text Solution
|