A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
WB JEE PREVIOUS YEAR PAPER-QUESTION PAPER 2021 -PHYSICS (CATEGORY -II)
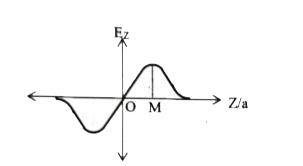
- The variation of electric field along the Z-axis due to a uniformly ch...
Text Solution
|
- Two metal wires of identical dimensions are connected in series. If si...
Text Solution
|
- A uniform rod of length L pivoted at one end P is freely rotated in a ...
Text Solution
|
- An ideal gas of molar mass contained in a very tall vertical cylindri...
Text Solution
|
- Under isothermal conditionss, two soap bubbles of radii a and b coales...
Text Solution
|
- The potential energy of a particle of mass 0.02 kg moving along x-axis...
Text Solution
|
- A particle of mass m and charge q moving with velocity v enters region...
Text Solution
|