Topper's Solved these Questions
PROBABILITY
OMEGA PUBLICATION|Exercise Important Questions from Miscellaneous Exercise |7 VideosPROBABILITY
OMEGA PUBLICATION|Exercise Multiple Choice Questions (MCQs) |15 VideosPRINCIPLE OF MATHEMATICAL INDUCTION
OMEGA PUBLICATION|Exercise Multiple Choice Questions|10 VideosRELATIONS AND FUNCTIONS
OMEGA PUBLICATION|Exercise M.C.Q|19 Videos
Similar Questions
Explore conceptually related problems
OMEGA PUBLICATION-PROBABILITY-Multiple Choice Questions (MCQs)
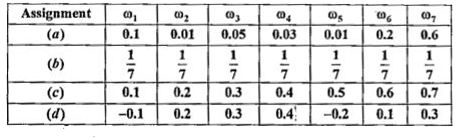
- Which of the following can not valid assignments for outcomes of sampl...
Text Solution
|
- A card is drawn from a pack of 100 cards numbered 1 to 100. The probab...
Text Solution
|
- If A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A cap B...
Text Solution
|
- If two event A and B are independent, then
Text Solution
|
- Two dice are thrown, the probability that the sum of the points on two...
Text Solution
|
- The probability that a person will hit target in shooting practice is ...
Text Solution
|
- A sample space consists of three mutually independent and equally like...
Text Solution
|
- The chance of throwing a total of 3 or 5 or 11 with two dice is
Text Solution
|
- The probability that a non-leap year has 53 Sundays is
Text Solution
|
- Three identical dice are rolled. The probability that the same number ...
Text Solution
|
- From a well-shuffled pack of 52 cards, 2 cards are drawn, the first be...
Text Solution
|
- The number of elements in a sample space, when a die rolled twice are
Text Solution
|
- What is the probability of sure event ?
Text Solution
|
- What will be the probability of an impossible event ? a. 0 b. 1 c. 2 d...
Text Solution
|
- The number of elements in a sample space when a coin is tossed and a d...
Text Solution
|
- The number of elements in a sample space, when coin is tossed four tim...
Text Solution
|