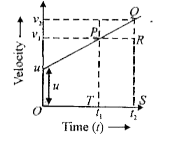
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Show that the slope of velocity-time graph for uniformly acceleratied ...
Text Solution
|
- Assertion: In a uniformly accelerated motion, acceleration the graph i...
Text Solution
|
- Assertion: The slope of displacement-time graph of a body moving with ...
Text Solution
|
- Show that the slope of displacement-time graph is equal to the velcoit...
Text Solution
|
- Assertion : Distance-time graph of the motion of a body having uniform...
Text Solution
|
- Asserion : The acceleration of an object at a particular time is the s...
Text Solution
|
- Draw velocity – time graph of uniformly accelerated motion in one dime...
Text Solution
|
- [" The acceleration of a "],[" moving body can be found "],[" from "],...
Text Solution
|
- 1.The acceleration of a moving body can be found from (A) Area under v...
Text Solution
|