Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
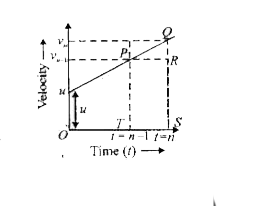
- Prove that distance travelled by a body in the n ^(th) second is S (n...
Text Solution
|
- Chek the correctness of the relation, S(n(th)) = u +(a)/(2)(2n -1), wh...
Text Solution
|
- With usual notation, the following equation, said to give the distance...
Text Solution
|
- For a particle moving with constant acceleration, prove that the displ...
Text Solution
|
- सिद्ध कीजिए कि एकसमान त्वरित पिंड द्वारा nवें सेकण्ड में तय की गई दूरी...
Text Solution
|
- A freely falling body travelled x m in n^("th") second. Then distance ...
Text Solution
|
- During the n th second of its motion a body covers a distance s(n) wit...
Text Solution
|
- A freely falling body traveled xm in n^(th) second distance travelled ...
Text Solution
|
- The distance travelled by a particle in n^(th) second is Sn =u+a/2 (2n...
Text Solution
|