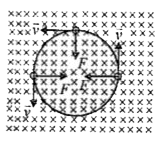
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find an expression for angular frequency when charged particle moves a...
Text Solution
|
- A charged particle having charge q, is moving at right angles to a mag...
Text Solution
|
- चुम्बकीय क्षेत्र में गतिमान आवेशित कण पर लगने वाले बल के लिए व्यंजक ज्...
Text Solution
|
- The angular frequency of a charged particle moving in a uniform magnet...
Text Solution
|
- When a charged particle moves perpendicular to a magnetic field, then:
Text Solution
|
- When a charged particle moves in a uniform magnetic field at right ang...
Text Solution
|
- What should be the angle between the velocity vector of the charged pa...
Text Solution
|
- A charged particle moves at right angles to a uniform magnetic field a...
Text Solution
|
- Magnetic Force on Charge||Path OF Charge Particle Moving Perpendicular...
Text Solution
|