Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
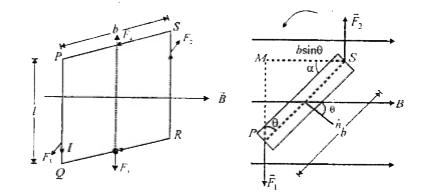
- Derive the expression for the torque acting on a current carrying loop...
Text Solution
|
- A rectangular loop carrying a current i is placed in a uniform magneti...
Text Solution
|
- Derive an expression for the magnetic field at a point on the axis of ...
Text Solution
|
- Derive an expression for torque on a current loop placed in a magnetic...
Text Solution
|
- What is the torque on a current carrying loop placed in a uniform magn...
Text Solution
|
- Derive an expression for the torque acting on a current carrying loop ...
Text Solution
|
- Derive an expression for the torque acting or a current carrying loop ...
Text Solution
|
- (a) Derive the expression for the torque acting on a current carrying ...
Text Solution
|
- Derive an expression for the torque acting on a rectangular current ca...
Text Solution
|