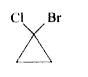To determine which of the given compounds is chiral, we will analyze each option for the presence of a plane of symmetry. A compound is considered chiral if it does not possess a plane of symmetry, meaning it cannot be superimposed on its mirror image.
### Step-by-Step Solution:
1. **Identify the Compounds**: We have four cyclic compounds labeled A, B, C, and D. We need to analyze each compound for chirality.
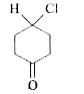
2. **Analyze Compound A**:
- Visualize compound A as a hexagonal ring with substituents (ketone, Cl, and H).
- A plane of symmetry can be drawn through the compound, dividing it into two equal halves.
- Since it has a plane of symmetry, compound A is **achiral**.
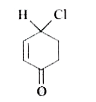
3. **Analyze Compound B**:
- Visualize compound B as a six-membered ring with a ketone, Cl, H, and a double bond.
- Attempt to draw a plane of symmetry. The presence of the double bond means that the two sides of the compound are not identical.
- There is no plane of symmetry that can bisect this compound into two equal halves.
- Therefore, compound B is **chiral**.
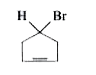
4. **Analyze Compound C**:
- Visualize compound C as a five-membered ring with H, Br, and a double bond.
- A plane of symmetry can be drawn through the compound, bisecting it into two equal halves.
- Since it has a plane of symmetry, compound C is **achiral**.
5. **Analyze Compound D**:
- Visualize compound D as a three-membered ring with Cl and Br.
- A plane of symmetry can also be drawn through this compound, dividing it into two equal halves.
- Since it has a plane of symmetry, compound D is **achiral**.
6. **Conclusion**: After analyzing all four compounds, we find that only compound B does not possess a plane of symmetry and is therefore chiral.
### Final Answer:
The chiral compound is **Option B**.