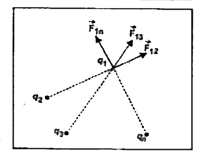
Principle of superposition of charges : According to this principle when a number of point charges interact in space then total force on a particular charge is the vector sum of forces exerted on it by all the other individual charges.
Consider that n point charges `q_1,q_2,q_3,........q_n` are distributed in space in a discrete manner. The charges are interacting with each other. Let us find the total force on charges say `q_1` due the all other remaining charges. If the charges `q_2, q_3, ...... q_n` exert forces `vecF_(12),vecF_(13),......vecF_(1n)` on the charge `q_1`, then, according to principle of uperposition, the total force on charge `q_1` given by
`vecF_(1)=vecF_(12)+vecF_(13)+......vecF_(1n) " "....(i)`
If the distance between the charges `q_1 and q_2` is `r_(12)` , and `hatr_(21)` is unit vector from charges `q_2 and q_2`, then
`vecF_(12)=1/(4piin_0).(q_1q_2)/(r_(12))hatr_(21)`
Similarly, the force on charge `q_1` due to other charges is given by
`vecF_(13)=1/(4piin_0).(q_1q_2)/(r_(13))hatr_(31)`
...............
................
and `vecF_(1n)=1/(4piin_0).(q_1q_n)/(r_(1n)^2)hatr_(n1)`
Hence, in equation (i), setting the values of `vecF_(12),vecF_(13) , ........vecF_(1n)` the total force on charge `q_1` due to all other charges is given by
`vecF_(1)=1/(4piin_0)((q_1q_2)/r_(12)^2hatr_(21)+(q_1q_3)/r_(13)^2hatr_(21)+.....(q_1q_2)/r_(1n)^2hatr_(nt))`
or `vecF_1=1/(4piin_0)sum_(i=1,j=1,"in"nej)^n(q_iq_j)/(r_(ij)^2)hatr_(ji)`