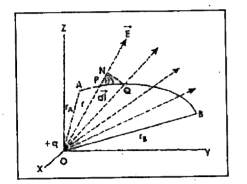
Consider a point charge +q located at the origin O. The electric field due to the point charge will be directed along the dotted arrows i.e, radially outwards from the point charge +q. Suppose that AB is any path (straight or curved) between two points A and B in the electric field of the point charge +q, such that `OA=r_(A)` and `OB=r_(B)`. Further, suppose that P is any point on the path AB and `vecE` is electric field due to the point charge f g at this point.
Let distance of point P from the point charge + q is `OP=r`. Let `vec(PQ)=vec(dl)` be very small displacement along the path AB. Since electric field `vecE` gives measure of force on a unit positive charge placed at point P,
`vecE.vec(dl)`= work done by the electric field `vecE` in moving a unit positive charge from point P to Qi.e., through `vec(PQ).(vec(dl))`
`int_(A)^(B)vecE.vec(dl)=` work done by the electric field `vecE` in moving a unit positive charge from the point A to B.
`int_(A)^(B)vecE.vec(dl)` is called the line integral of the electric field `vecE` between the points A and B. now find the value of integral `int_(A)^(B)vecE.vec(dl)`.
Electric field at point P due to point charge +q located at the point O is given
`vecE=(1)/(4piin_(0)).(q)/(r^(2))hatr`
where `hatr` is a unit vector along the line OP. If `theta` is angle between the direction of `vecE` and `vec(dl)`
`vecE.vec(dl)=(1)/(4piin_(0)).(q)/(r^(2))hatr.vec(dl)=(1)/(4piin_(0)).(q)/(r^(2))(1)(dl)costheta`
or `vecE.vec(dl)=(1)/(4piin_(0)).(q)/(r^(2))(dl)costheta" "......(1)`
From point Q, drop ON perpendicular to OP. Then, from right angled `DeltaPNQ`, we have
`PN=PQcostheta=dlcostheta`
Further, as PN (the projection of `vec(dl)` along the line OP) is in the direction of increasing r, the distance PN is taken as + dr. Therefore,
`dlcostheta=vec(dr)`
setting `dlcostheta=dr` in equation (1), we have
`vecE.vec(dl)=(1)/(4piin_(0))(q)/(r^(2))dr`
Hence, `int_(A)^(B)vecE.vec(dl)=int_(A)^(B)(1)/(4piin_(0)).(q)/(r^(2))dr=(1)/(4piin_(0)).qint_(A)^(B)r^(-2)dr" ".....(2)`
The values of r corresponding to points A and B are `r_(A)` and `r_(B)` respectively. Therefore, in equation (2) corresponding to the limits from A to B, the proper limits of integration are from `r_(B)` to `r_(B)`. Likewise, equation (2) becomes
`int_(A)^(B)vecE.vec(dl)=(1)/(4piin_(0)).qint_(r_(A))^(r_(B))r^(-2)dr=(1)/(4piin_(0))q|(r^(-1))/(-1)|_(r_(B))^(r_(B))=(1)/(4piin_(0))q|-(1)/(r)|_(r_(A))^(r_(B))`
`=(1)/(4piin_(0)).q|-(1)/(r_(B))-(-(1)/(r_(A)))|`
or `int_(A)^(B)vecE.vec(dl)=(1)/(4piin_(0)).q((1)/(r_(A))-(1)/(r_(B)))" "......(3)`
The equation (3) gives the value of line integral of the electric field between two points and B along the path AB shown in Fig. above. It follows that the expression depends only on the distances of the end points A and B (i.e., `r_(A)` and `r_(B)` ) and not upon the path AB.
Hence, the line integral of the electric field between two points is same for all the paths between the two points i.e., it is independent of the path followed between the two points.
