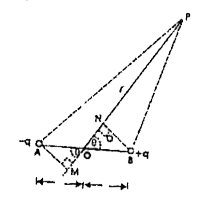
Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|16 VideosELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS |7 VideosELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)|9 VideosELECTRONIC DEVICES SOLIDS
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|9 VideosFORCE ON A CHARGE
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |14 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-ELECTROSTATIC POTENTIAL-LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)
- Define electric potential. What is the SI unit of potential? Obtain an...
Text Solution
|
- Show that work done in moving an electric charge between any two point...
Text Solution
|
- Define potential difference between two points in an electrostatic fie...
Text Solution
|
- Give the physical meaning of electrostatic potential?
Text Solution
|
- Obtain an expression for potential energy of the configuration of thr...
Text Solution
|
- What is electric potential enerrgy due to a system of charges? Derive ...
Text Solution
|
- What is the direction of electric field at a point on the equitorial l...
Text Solution
|
- Show mathematically that the potential at a point on the equitorial li...
Text Solution
|