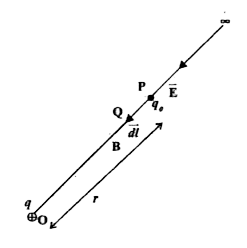
Let us consider a point charge +q located at O, as shown in Fig. Supposė at any instant the test charge `q_(0)` is at a point P such that
`vec(OP)=vecr`. Let `vecE` be the electric field at P due to charge + q. So the force on the test charge
`q_(0)` is `q_(0)vecE`. Hence an external force `-q_(0)vecE` is required to displace the test charge against the field.
In displacing the test charge `q_(0)` through a small displacement `vec(PQ)=vec(dl)`, one needs to do a small amount of work, given by
`dW=vecF.vec(dl)=-q_(0)vecE.vec(dl)`
If the test charge is moved from A to B, total work done is given by
`W_(AB)=intdW=-q_(0)int_(A)^(B)vecE.vec(dl)`
The work done in moving a unit positive charge from A to B, or by definition, the potential difference between points A and B will be
`V_(B)-V_(A)=(W_(AB))/(q_(0))=-int_(A)^(B)vecE.vec(dl)`
That is, the potential difference between two points A and B is equal to the negative of the line integral of the electrostatic field along the path AB.
If point A at infinity, where potential `V_(A)= 0`, the potential at point B is given by
`V_(B)=-int_(oo)^(B)vecE.vec(dl)`
Potential at any point with position vector `vecr` is
`V=-int_(A)^(B)vecE.vec(dl)`
Thus, the electric potential at any point is equal to the negative of the line integral of the electrostatic field from infinity to that point.