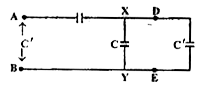
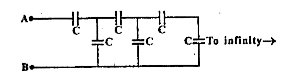Text Solution
Verified by Experts
Topper's Solved these Questions
CAPACITANCE
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS|9 VideosCAPACITANCE
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS (3/4 Marks Questions)|2 VideosCAPACITANCE
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |21 VideosALTERNATING CURRENTS
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS|11 VideosCLASSIFICATION OF MATERIALS
BETTER CHOICE PUBLICATION|Exercise Most expected question (2 marks)|3 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-CAPACITANCE -MOST EXPECTED NUMERICALS
- Connect three capacitors of 3 muF, 3 muF and 6 muF such that their equ...
Text Solution
|
- Three capacitors are having capacity in the ratio of 1 : 2 : 3. Their ...
Text Solution
|
- Calculate the equivalent capacitance of the combination between the po...
Text Solution
|
- A metal of radius of 1 cm can not hold a charge of 1 coulomb. Why?
Text Solution
|
- Find the equivalent capacitance between the terminals A and B in the g...
Text Solution
|