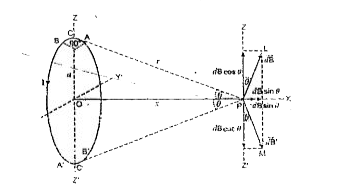
Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETIC EFFECTS OF CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICALS PROBLEMS |3 VideosMAGNETIC EFFECTS OF CURRENT
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|4 VideosMAGNETIC DIPOLES AND EARTH'S MAGNETISM
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|8 VideosNUCLEAR REACTIONS
BETTER CHOICE PUBLICATION|Exercise Numerical Problems|9 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-MAGNETIC EFFECTS OF CURRENT-LONG ANSWER TYPE QUESTIONS
- Using Ampere's circuital law, derive an expression for the magnetic fi...
Text Solution
|
- Using Ampere's circuital law, derive an expression for the magnetic fi...
Text Solution
|
- Derive an expression for magnetic field at the centre of circular curr...
Text Solution
|
- The magnetic field at a point due to a current carrying conductor is d...
Text Solution
|
- State the Biot-Savart's law for the magnetic field due to a current ca...
Text Solution
|
- Derive an expression for magnetic field at the centre of circular curr...
Text Solution
|
- Derive an expression for magnetic field at the centre of circular curr...
Text Solution
|
- Write expression for the magnetic flux density at a point due to a cur...
Text Solution
|
- Write expression for the magnetic flux density at a point due to a cur...
Text Solution
|
- State Ampere's circuital law. By using it derive an expression for mag...
Text Solution
|
- State Ampere's circuital law. By using it derive an expression for mag...
Text Solution
|
- State Ampere's circuital law. By using it derive an expression for mag...
Text Solution
|
- State the rule that is used to find the direction of field acting at a...
Text Solution
|
- Using Ampere's circuital theorem, calculate the magnetic field due to ...
Text Solution
|
- What is Maxwell's right hand thumb rule?
Text Solution
|
- State Biot-Savart law. Using Biot-Savart law find the magnitude and di...
Text Solution
|