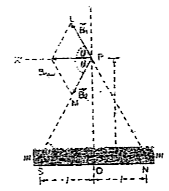
Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETIC DIPOLES AND EARTH'S MAGNETISM
BETTER CHOICE PUBLICATION|Exercise Long answer type questions|18 VideosMAGNETIC DIPOLES AND EARTH'S MAGNETISM
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|8 VideosMAGNETIC DIPOLES AND EARTH'S MAGNETISM
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|8 VideosINTERFERENCE OF LIGHT
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS (1 Mark)|3 VideosMAGNETIC EFFECTS OF CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICALS PROBLEMS |3 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-MAGNETIC DIPOLES AND EARTH'S MAGNETISM-Short Answer Type Questions
- What is probable cause of earth's magnetism?
Text Solution
|
- Define angle of magnetic inclination at a plane.
Text Solution
|
- What happens if a bar magnet is cut into pieces along its length?
Text Solution
|
- What will happen to the dipole moment, if a bar magnet is cut into equ...
Text Solution
|
- Derive an expression for torque acting on a bar magnet placed in a uni...
Text Solution
|
- State four properties of a bar magnet.
Text Solution
|
- Deduce the expression for the magnetic dipole moment of an electron or...
Text Solution
|
- Derive an expression for the torque expereinced by a amgnetic dipole s...
Text Solution
|
- What is magnetic dipole? Derive an expression for magnetic field inten...
Text Solution
|
- What is magnetic dipole? Derive an expression for magnetic field inten...
Text Solution
|