Text Solution
Verified by Experts
Topper's Solved these Questions
OPTICAL INSTRUMENTS
BETTER CHOICE PUBLICATION|Exercise NUMERICALS PROBLEMS |15 VideosOPTICAL INSTRUMENTS
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS |12 VideosNUCLEAR REACTIONS
BETTER CHOICE PUBLICATION|Exercise Numerical Problems|9 VideosPARTICLE NATURE OF RADIATION
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |32 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-OPTICAL INSTRUMENTS-LONG ANSWER TYPE QUESTIONS
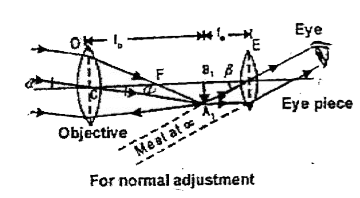
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- What is the magnifying power of an astronomical telescope when the fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- What is the magnifying power of an astronomical telescope when the fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- What is the magnifying power of an astronomical telescope when the fin...
Text Solution
|
- Explain the construction and working of an astronomical telescope. fin...
Text Solution
|
- Draw the course of rays in an astronomical telescope, when the final i...
Text Solution
|
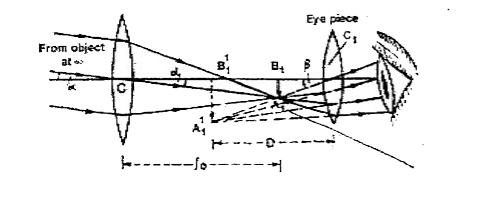
- Draw a ray diagram to show image formation in a compound microscope. F...
Text Solution
|
- Define the magnifying power of compound microscope.
Text Solution
|
- Draw a ray diagram to show image formation in a compound microscope. F...
Text Solution
|
- Draw the ray diagram of acompound microscope.
Text Solution
|
- Define the magnifying power of compound microscope.
Text Solution
|
- Draw a ray diagram to show image formation in a compound microscope. F...
Text Solution
|
- Draw a ray diagram of compound microscope for the final image formed a...
Text Solution
|
- Draw a ray diagram of compound microscope for the final image formed a...
Text Solution
|
- Draw a labelled ray diagram of a compound microscope. Explain its work...
Text Solution
|