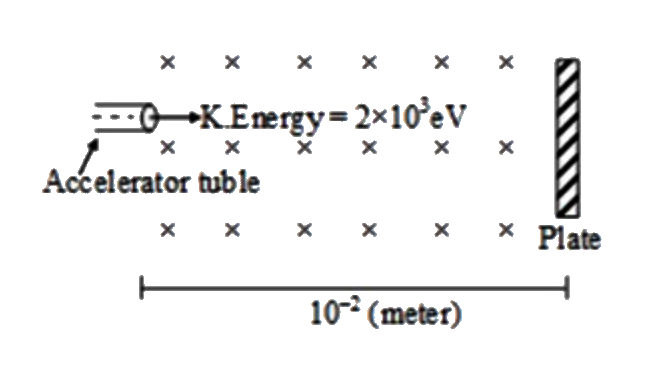A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A charged particle having a mass of 1.6xx10^(-26) kg comes out of acce...
Text Solution
|
- A beam of charged particle, having kinetic energy 10^3 eV , contains m...
Text Solution
|
- A charged particle of mass m and charge q is released from rest in an ...
Text Solution
|
- द्रव्यमान m आवेश q तथा गतिज ऊर्जा K का एक कण एकसमान चुंबकीय क्षेत्र B ...
Text Solution
|
- The electric field that can balance a charged particle of mass 3.2xx10...
Text Solution
|
- Positively charged particles are projected into a magnetic field. If t...
Text Solution
|
- q आवेश तथा m द्रव्यमान का एक आवेशित कण चुंबकीय क्षेत्र B में लंबवत प्र...
Text Solution
|
- A charged particle having a mass of 1.6xx10^(-26) kg comes out of acce...
Text Solution
|
- (A) : A charged particle can be accelerated in a cyclotron by the osci...
Text Solution
|