Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-GRAVITATION-Exercise 5 B (Previous Year Questions)
- A satellite S is moving in an elliptical orbit around the earth. The m...
Text Solution
|
- A geo-stationary satellite orbits around the earth in a circular orbit...
Text Solution
|
- A double star system consists of two stars A and B which have time per...
Text Solution
|
- Two bodies, each of mass M, are kept fixed with a separation 2L. A par...
Text Solution
|
- A planet of radius R=1/10 (radius of the Earth) has the same mass den...
Text Solution
|
- Assertion: An astronaut in an orbiting space station above the earth e...
Text Solution
|
- A projectile is fired vertically up from the bottom of a crater (big h...
Text Solution
|
- A bullet is fired vertically upwards with velocity v from the surface ...
Text Solution
|
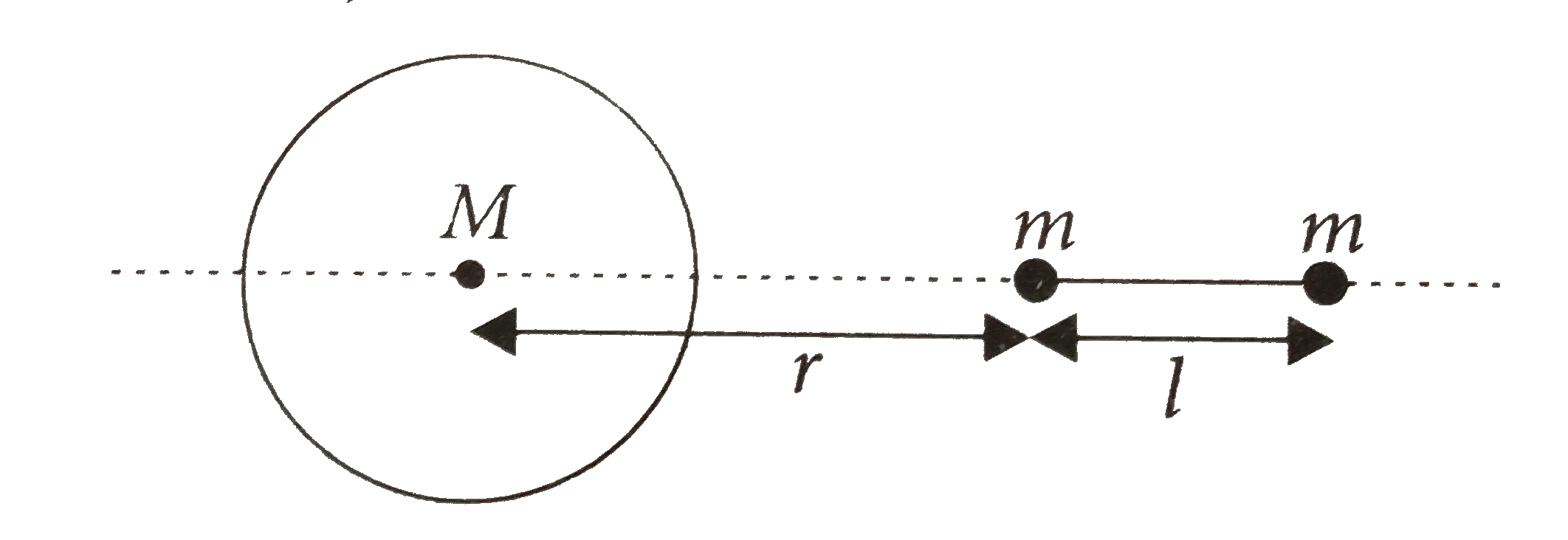
- A large spherical mass M is fixed at one position and two identical po...
Text Solution
|
_E01_144_S01.png)