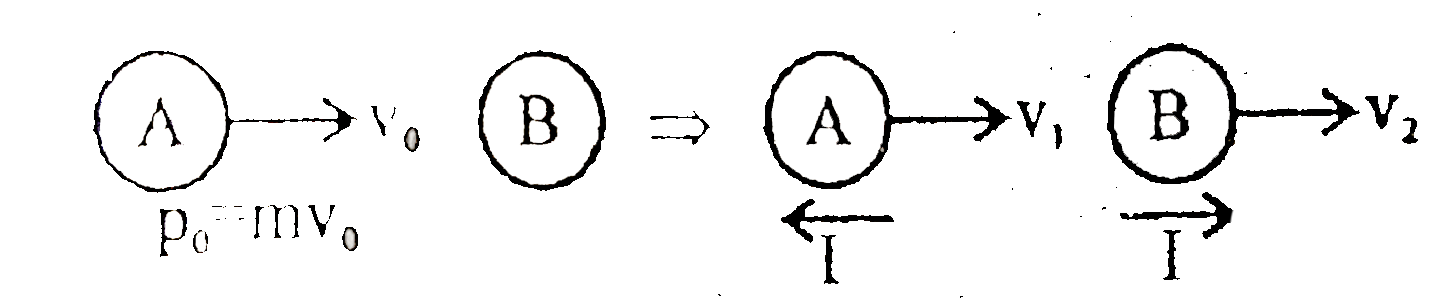A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-TEST PAPERS-MATHS
- In a head on collision between two identical particles A and B moving ...
Text Solution
|
- If complex number z(z!=2) satisfies the equation z^2=4z+|z|^2+(16)/(|z...
Text Solution
|
- If the function f(x)={{:((1+cospix)/(pi^(2)(x+1)^(2)),",",xlt-1),(ax...
Text Solution
|
- The value of the following limit lim(ntooo) n(n+1)(ln(1+(1)/(n))-sin((...
Text Solution
|
- If f(x)=|x-1|.([x]=[-x]), then (where [.] represents greatest integer ...
Text Solution
|
- If b be the foot of perpendicular from A to the plane rcdothat(n)=d, t...
Text Solution
|
- A transversal cuts side AB and AD and diagonal AC of parallelogram ABC...
Text Solution
|
- The x-intercept of the tangent to a curve is equal to the ordinate of ...
Text Solution
|
- A function y=f(x) satisfies A function y=f(x) satisfies f" (x)= -1/x^...
Text Solution
|
- Let (1+x^2)^2(1+x)^n=sum(k=0)^(n+4)ak x^k. If a1, a2 and a3 are in ari...
Text Solution
|
- If f(x) is double differentiable function such that |f"(x)|le5 for ea...
Text Solution
|
- overline(x)andoverline(y) be two variable vectors satisfying simultan...
Text Solution
|
- The area bounded by the curve y=x^2+2x+1 and tangent at (1, 4) and y...
Text Solution
|
- In a problem of differentiation of (f(x))/(g(x)), one student writes ...
Text Solution
|
- Ratio of amplitude for two wave is 5:9 .Find the ratio of intensity?
Text Solution
|