Text Solution
Verified by Experts
Topper's Solved these Questions
CENTRE OF MASS
ALLEN|Exercise EXERCISE-I|40 VideosCENTRE OF MASS
ALLEN|Exercise EXERCISE-II|43 VideosBASIC MATHEMATICS USED IN PHYSICS &VECTORS
ALLEN|Exercise EXERCISE-IV ASSERTION & REASON|11 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN|Exercise Exercise 5 B (Integer Type Questions)|3 Videos
Similar Questions
Explore conceptually related problems
ALLEN-CENTRE OF MASS-EXERCISE-V B
- A drum major's baton consists of two masses m(1) and m(2) separated by...
Text Solution
|
- Two particles of mases m(1) and m(2) in projectile motion have velocit...
Text Solution
|
- Two blocks of masses 10 kg and 4 kg are connected by a spring of negli...
Text Solution
|
- A particle moves in the xy plane under the influence of a force such t...
Text Solution
|
- Two small particles of equal masses start moving in opposite direction...
Text Solution
|
- Look at the drawing given in the figure which has been drawn with ink ...
Text Solution
|
- A particle of mass m is projected from the ground with an initial spee...
Text Solution
|
- A tennis ball dropped on a horizontal smooth surface , it because back...
Text Solution
|
- Two balls having linear momenta vecp(1)=phati and vecp(2)=-phati, und...
Text Solution
|
- Assertion: In and elastic collision between two bodies, the relative s...
Text Solution
|
- Statement-1: if there is no external torque on a body about its centre...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- Two blocks of masses 2kg and M are at rest on an inclined plane and ar...
Text Solution
|
- A car P is moving with a uniform speed 5sqrt(3) m//s towards a carriag...
Text Solution
|
- A particle of mass m, moving in a circular path of radius R with a co...
Text Solution
|
- Two point masses m1 and m2 are connected by a spring of natural length...
Text Solution
|
- A rectangular plate of mass m and dimension a × b is held in horizonta...
Text Solution
|
- Three objects A, B and C are kept in a straight line on a frictionless...
Text Solution
|

 From the sketch we see that `r_(1) = r_(1) - R`
From the sketch we see that `r_(1) = r_(1) - R` 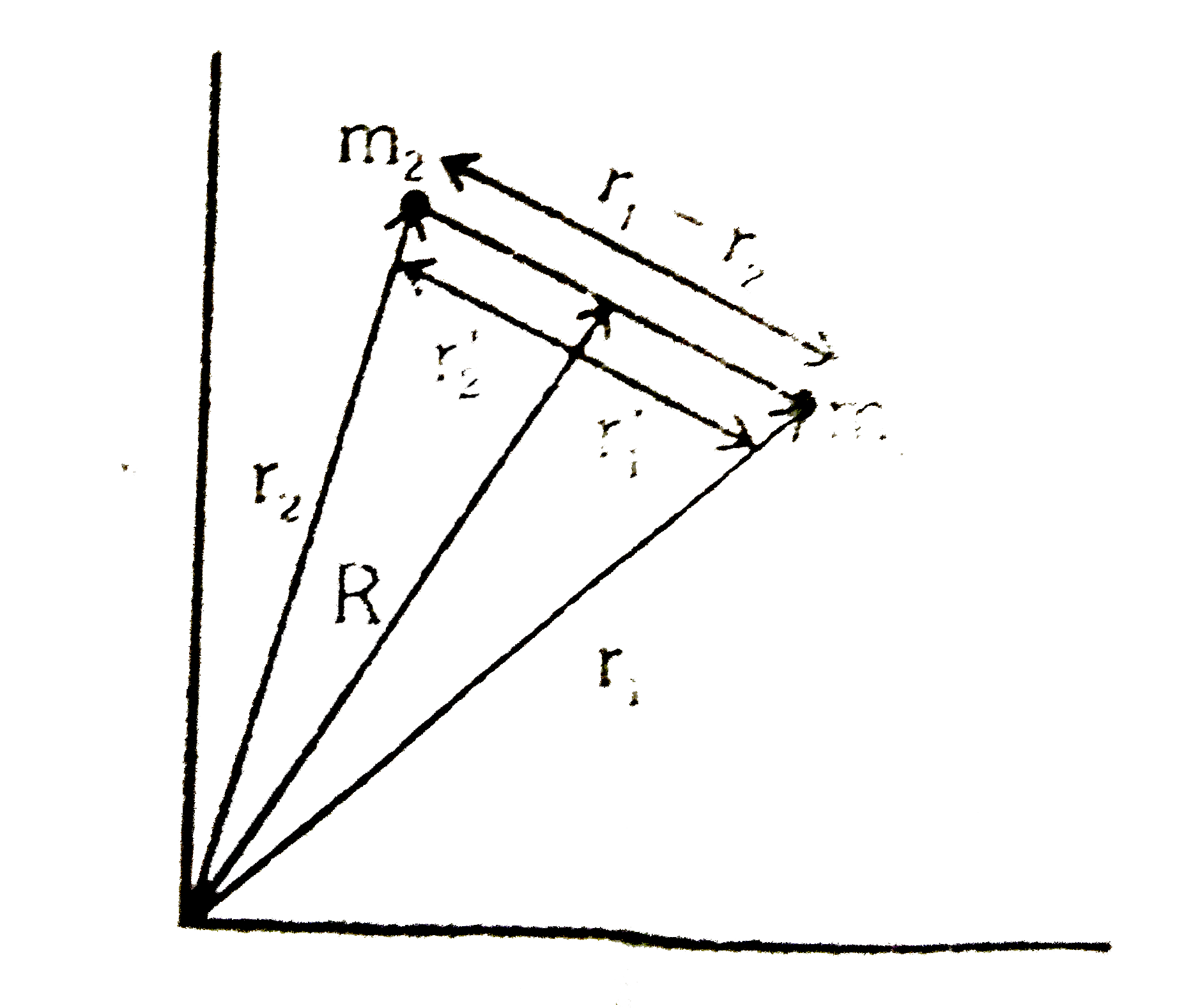
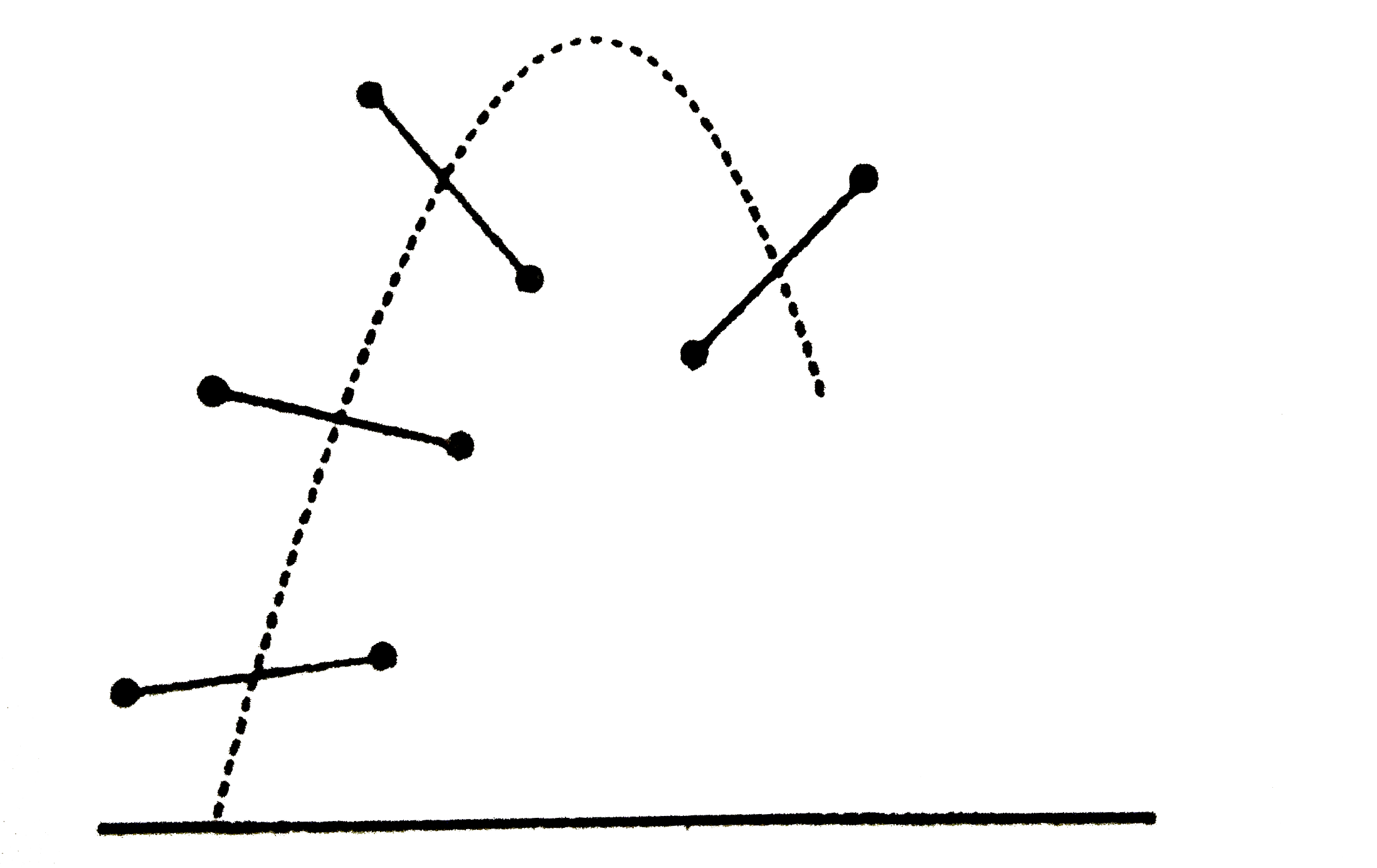 The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.
The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.