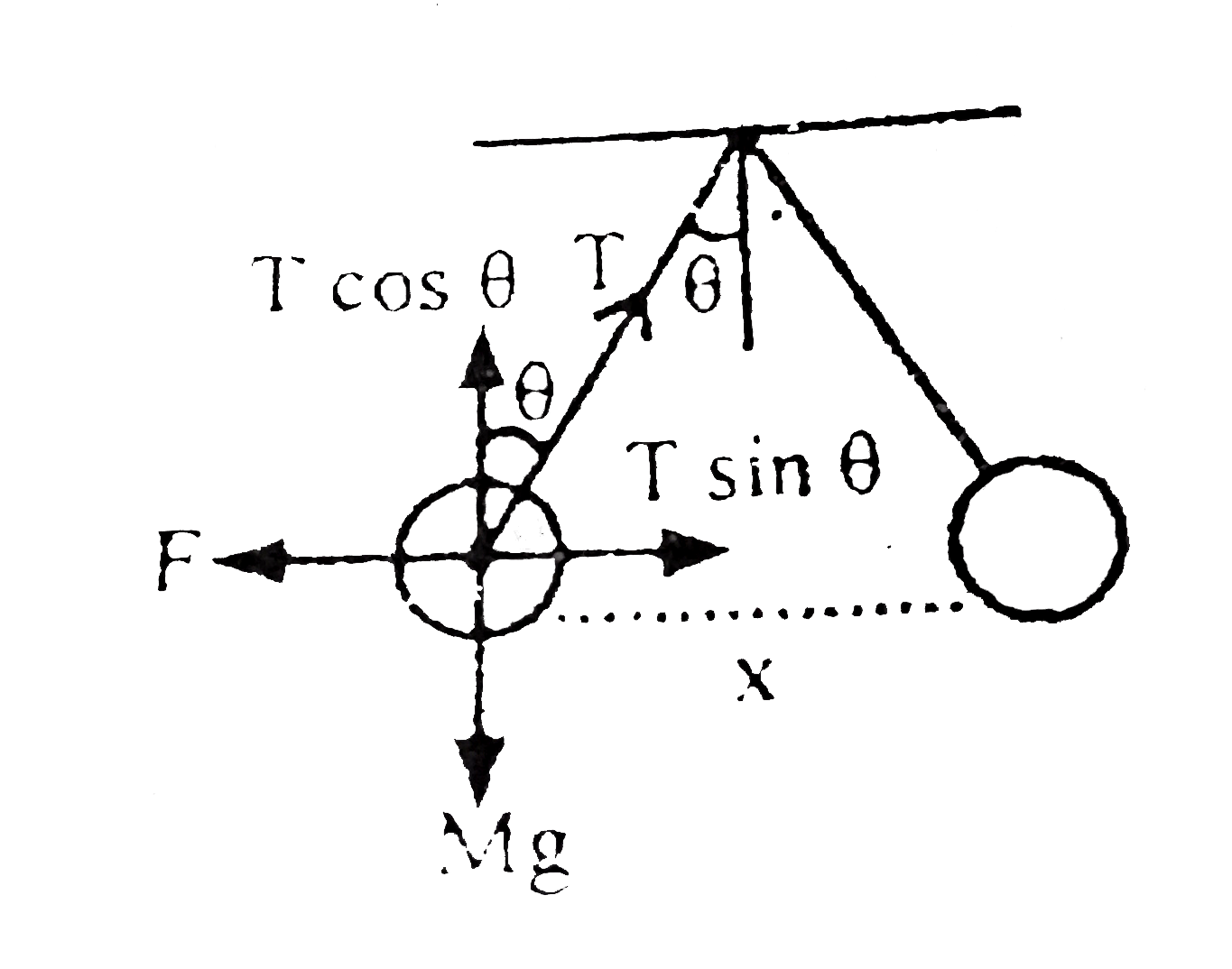
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS
ALLEN|Exercise Exercise-05(B)|19 VideosMISCELLANEOUS
ALLEN|Exercise MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER|6 VideosMISCELLANEOUS
ALLEN|Exercise Exersice-04[B]|16 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN|Exercise BEGINNER S BOX-7|8 VideosPHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
ALLEN|Exercise EXERCISE-IV|8 Videos
Similar Questions
Explore conceptually related problems
ALLEN-MISCELLANEOUS-Exercise-05(A)
- A charge Q is placed at each of the opposite corners of a square. A ch...
Text Solution
|
- This question contains statements-1 and Statement-2. Of the four choic...
Text Solution
|
- Two points P and Q are maintained at the potentials of 10V and -4V res...
Text Solution
|
- Let P(r) = (Q)/(pi R^(4)) r be the charge desntiy distribution for a s...
Text Solution
|
- Charge q is uniformly distributed over a thin half ring of radius R. T...
Text Solution
|
- Let there be a spherically symmetric charge distribution with charge d...
Text Solution
|
- Two identical charged sphere are suspended by strings of equal length....
Text Solution
|
- Two identical charged spheres suspended from a common point by two mas...
Text Solution
|
- The electrostatic potential inside a charged spherical ball is given b...
Text Solution
|
- Two positive charges of magnitude q are placed at the ends of a side A...
Text Solution
|
- An insulating solid sphere of radius R has a uniform positive charge d...
Text Solution
|
- In a uniformly charged sphere of total charge Q and radius R, the elec...
Text Solution
|
- Two charges, each equal to q, are kept at x = −a and x = a on the x-ax...
Text Solution
|
- A charge Q is uniformly distributed over a long rod AB of length L as ...
Text Solution
|
- Assume that an electric field E=30 x^(2) hat(i) exist in space. Then, ...
Text Solution
|
- A uniformly charged solid sphere of radius R has potential V(0) (meas...
Text Solution
|
- A long cylindrical shell carries positive surface charge sigma in the ...
Text Solution
|
- The region between two concentric spheres of radii a and b (gt a) cont...
Text Solution
|
- The potential (in volts) of a charge distribution is given by V(z)=3...
Text Solution
|
- Within a spherical charge distribution of charge density rho(r), N equ...
Text Solution
|