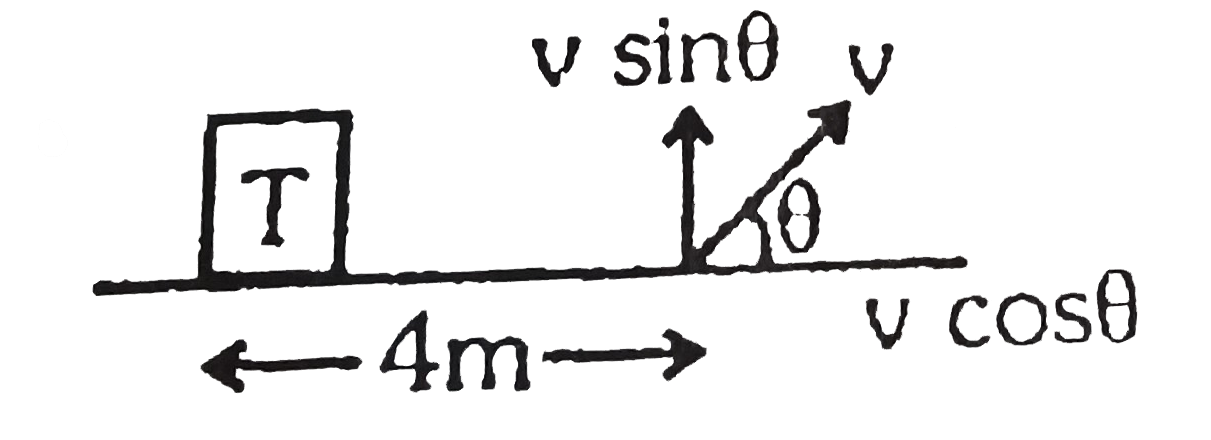Home
Class 11
PHYSICS
The position vector of a particle is giv...

The position vector of a particle is given as `vec(r)=(t^(2)-4t+6)hat(i)+(t^(2))hat(j)`. The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to

A

1 sec

B

2 sec

C

1.5 sec

D

Not possible

Text Solution

Verified by Experts

The correct Answer is:
A
`vec(r)=(t^(2)-4t+6)hat(i)+t^(2)hat(j), vec(v)=(2t-4)hat(i)+2t hat(j)`
`vec(a)=2(hati+hatj)`, when `vec(a) bot vec(v)` then `vec(a).vec(v)=0, t=1 s`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    ALLEN|Exercise EXERCISE-03|6 Videos

  • KINEMATICS

    ALLEN|Exercise Assertion-Reason|20 Videos

  • KINEMATICS

    ALLEN|Exercise EXERCISE-01|55 Videos

  • ERROR AND MEASUREMENT

    ALLEN|Exercise Part-2(Exercise-2)(B)|22 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN|Exercise BEGINNER S BOX-7|8 Videos

Similar Questions

Explore conceptually related problems

The position vector of a aprticle is given as vecr=(t^2-4t+6)hati+(t^2)hatj . The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to

The position vector of a aprticle is given as vecr=(t^2-4t+6)hati+(t^2)hatj . The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to

The position vector of a particle of mass m= 6kg is given as vec(r)=[(3t^(2)-6t) hat(i)+(-4t^(3)) hat(j)] m . Find: (i) The force (vec(F)=mvec(a)) acting on the particle. (ii) The torque (vec(tau)=vec(r)xxvec(F)) with respect to the origin, acting on the particle. (iii) The momentum (vec(p)=mvec(v)) of the particle. (iv) The angular momentum (vec(L)=vec(r)xxvec(p)) of the particle with respect to the origin.

The position vector of a particle is given by vec(r)=1.2 t hat(i)+0.9 t^(2) hat(j)-0.6(t^(3)-1)hat(k) where t is the time in seconds from the start of motion and where vec(r) is expressed in meters. For the condition when t=4 second, determine the power (P=vec(F).vec(v)) in watts produced by the force vec(F)=(60hat(i)-25hat(j)-40hat(k)) N which is acting on the particle.

The position vector of a particle moving in x-y plane is given by vec(r) = (A sinomegat)hat(i) + (A cosomegat)hat(j) then motion of the particle is :

Position vector of a particle is expressed as function of time by equation vec(r)=2t^(2)+(3t-1) hat(j) +5hat(k) . Where r is in meters and t is in seconds.

The position of of a particle is given by vec r =3.0 t hat I + 2.0 t^(2) hat j+ 5.0 hat k wher (t) in seconds and the coefficients have the proper units . Find the velocity and acceleration of the particle in magnitude and direction at time t=3.0 s

The position vector of a particle vec(R ) as a funtion of time is given by: vec(R )= 4sin(2pit)hat(i)+4cos(2pit)hat(j) Where R is in meters, t is in seconds and hat(i) and hat(j) denote until vectors along x-and y- directions, respectively Which one of the following statements is wrong for the motion of particle ?

The position vector of a particle is determined by the expression vec r = 3t^2 hat i+ 4t^2 hat j + 7 hat k . The displacement traversed in first 10 seconds is :

Position vector of a particle moving in space is given by : vec(r)=3sin t hat i+3 cos t hatj+4 t hatk Distance travelled by the particle in 2s is :

ALLEN-KINEMATICS-EXERCISE-02
  1. In the diagram shown, the displacement of particles is given as a func...

    Text Solution

    |

  2. Two trains, which are moving along different tracks in opposite direct...

    Text Solution

    |

  3. The position vector of a particle is given as vec(r)=(t^(2)-4t+6)hat(i...

    Text Solution

    |

  4. A 2m wide truck is moving with a uniform speed v(0)=8m//s along a stra...

    Text Solution

    |

  5. If some function say x varies linearly with time and we want to find i...

    Text Solution

    |

  6. A point move with uniform acceleration and upsilon(1), upsilon(2) and ...

    Text Solution

    |

  7. A particle starts from rest with constant acceleration. The ratio of s...

    Text Solution

    |

  8. A particle moves along a straight line OX. At a time t (in seconds) th...

    Text Solution

    |

  9. A ball is dropped from the top of a building the ball takes 0.5 s to f...

    Text Solution

    |

  10. A particle is thrown upwards from ground. It experiences a constant re...

    Text Solution

    |

  11. Drops of water fall from the roof of a building 9 m highat regular int...

    Text Solution

    |

  12. A disc in which several grooves are cut along the chord drawn from a p...

    Text Solution

    |

  13. Two boats A and B are moving along perpendicular paths in a still lake...

    Text Solution

    |

  14. A trolley was moving horizontally on a smooth ground with velocity v w...

    Text Solution

    |

  15. A particle P is projected from a point on the surface of a smooth incl...

    Text Solution

    |

  16. A particle is projected from a point P(2,0,0) m with a velocity 10 m//...

    Text Solution

    |

  17. A body is thrown horizontally with a velocity sqrt(2gh) from the top o...

    Text Solution

    |

  18. A particle A is projected with speed V(A) from a point making an angle...

    Text Solution

    |

  19. A body is projected at time t = 0 from a certain point on a planet's s...

    Text Solution

    |

  20. A particle moves in x-y plane and at time t is at the point (t^2, t^3 ...

    Text Solution

    |